Đề 14 thi thử kỳ thi thpt quốc gia môn : Toán thời gian làm bài 180 phút

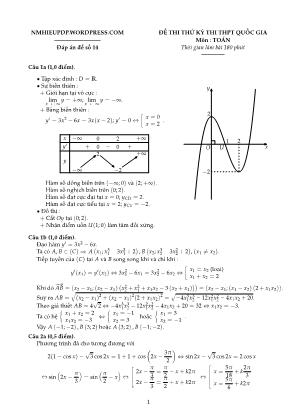
NMHIEUPDP.WORDPRESS.COM ĐỀ THI THỬ KỲ THI THPT QUỐC GIA
———————— Mụn : TOÁN
Đỏp ỏn đề số 14 Thời gian làm bài 180 phỳt
————
Cõu 1a (1,0 điểm).
• Tập xỏc định : D = R.
• Sự biến thiờn :
+ Giới hạn tại vụ cực :
lim
x→+∞ y = +∞; limx→−∞ y = −∞.
+ Bảng biến thiờn :
y′ = 3x2 − 6x = 3x(x− 2); y′ = 0⇔
ủ
x = 0
x = 2 .
x −∞ 0 2 +∞
y′ + 0 − 0 +
y
−∞
2
−2
+∞
Hàm số đồng biến trờn (−∞; 0) và (2;+∞).
Hàm số nghịch biến trờn (0; 2).
Hàm số đạt cực đại tại x = 0; yCĐ = 2.
Hàm số đạt cực tiểu tại x = 2; yCT = −2.
• Đồ thị :
+ Cắt Oy tại (0; 2).
+ Nhận điểm uốn U(1; 0) làm tõm đối xứng.
y
xO
2
−2
1 2
U
Cõu 1b (1,0 điểm).
Đạo hàm y′ = 3x2 − 6x.
Ta cú A, B ∈ (C)⇒ A Äx1; x31 − 3x21 + 2ọ , B Äx2; x32 − 3x22 + 2ọ, (x1 6= x2).
Tiếp tuyến của (C) tại A và B song song khi và chỉ khi :
y′(x1) = y′(x2)⇔ 3x21 − 6x1 = 3x22 − 6x2 ⇔
ủ
x1 = x2 (loại)
x1 + x2 = 2
Khi đú
−→
AB =
Ä
x2 − x1; (x2 − x1)
Ä
x22 + x
2
1 + x1x2 − 3 (x2 + x1)
ọọ
= (x2 − x1; (x1 − x2) (2+ x1x2)).
Suy ra AB =
√
(x2 − x1)2 + (x2 − x1)2(2+ x1x2)2 =
ằ
−4x31x32 − 12x21x22 − 4x1x2 + 20.
Theo giả thiết AB = 4
√
2⇔ −4x31x32 − 12x21x22 − 4x1x2 + 20 = 32⇔ x1x2 = −3.
Ta cú hệ
đ
x1 + x2 = 2
x1x2 = −3 ⇔
đ
x1 = −1
x2 = 3
hoặc
đ
x1 = 3
x2 = −1 .
Vậy A (−1;−2) , B (3; 2) hoặc A (3; 2) , B (−1;−2).
Cõu 2a (0,5 điểm).
Phương trỡnh đó cho tương đương với
2(1− cos x)−
√
3 cos 2x = 1+ 1+ cos
ầ
2x− 3pi
2
ồ
⇔ sin 2x−
√
3 cos 2x = 2 cos x
⇔ sin
Å
2x− pi
3
ó
= sin
Åpi
2
− x
ó
⇔
 2x−
pi
3
=
pi
2
− x+ k2pi
2x− pi
3
=
pi
2
+ x+ k2pi
⇔
 x =
5pi
18
+ k
2pi
3
x =
5pi
6
+ k2pi
1
Vậy phương trỡnh cú cỏc nghiệm trờn khoảng (0;pi) là x =
5pi
6
, x =
5pi
18
, x =
17pi
18
.
Cõu 2b (0,5 điểm).
Gọi z = ai+ b (a, b ∈ R), ta cú :
z+ 2z = (1+ 5i)2 ⇔ a+ bi+ 2 (a− bi) = −24+ 10i⇔
đ
a = −8
b = −10
Vậy z = −8− 10i.
Cõu 3 (0,5 điểm).
Với điều kiện 1 < x < 3, phương trỡnh đó cho tương đương với :
log2(x+ 1) + log2(3− x) = log2(x− 1)⇔ log2 [(x+ 1)(3− x)] = log2(x− 1)
⇔ −x2 + 2x+ 3 = x− 1
⇔
 x =
1+
√
17
2
x =
1−√17
2
(loại)
Vậy phương trỡnh cú nghiệm x =
1+
√
17
2
.
Cõu 4 (1,0 điểm).
Xột hệ phương trỡnh
x
2 + y2 − xy+ 4y+ 1 = 0 (1)
y
(
7− (x− y)2
)
= 2
Ä
x2 + 1
ọ
(2)
.
Từ (1) ta cú x2 + 1 = −y2 + xy− 4y thay vào (2) ta cú
y
(
7− (x− y)2
)
= 2
Ä−y2 + xy− 4yọ⇔ y (2 ((x− y)− 4)− 7+ (x− y)2) = 0
⇔
ủ
y = 0
(x− y)2 + 2 (x− y)− 15 = 0
⇔
 y = 0x− y = 3
x− y = −5
Với y = 0 thay vào (1) được x2 + 1 = 0 (vụ nghiệm).
Với x = y+ 3 thay vào (1) được y2 + 7y+ 10 = 0⇔
ủ
y = −2
y = −5 ⇒
ủ
x = 1
x = −2 .
Với x = y− 5 thay vào (1) được y2 − y+ 26 = 0 (vụ nghiệm).
Vậy hệ đó cho cú hai nghiệm (x; y) = (1;−2) và (x; y) = (−2;−5).
Cõu 5 (1,0 điểm).
Ta cú I =
1∫
0
x3
(√
x2 + 1− x
)
x2 + 1− x2 dx =
1∫
0
x3
ằ
x2 + 1dx−
1∫
0
x4dx = I1 − x
5
5
∣∣∣∣∣
1
0
= I1 − 15 .
Đặt u =
√
x2 + 1⇔ u2 = x2 + 1⇒ udu = xdx.
Đổi cận x = 0⇒ u = 1, x = 1⇒ u = √2, ta cú :
I1 =
√
2∫
1
Ä
u2 − 1ọ u.udu = √2∫
1
Ä
u4 − u2ọdu = (u5
5
− u
3
3
)∣∣∣∣∣
√
2
1
=
2
√
2+ 2
15
Vậy I =
2
√
2+ 2
15
− 1
5
=
2
√
2− 1
15
.
2
Cõu 6 (1,0 điểm).
Hỡnh thoi ABCD cúữBAD = 600 ⇒ ∆ABD đều cạnh a.
Gọi O = AC ∩ BD ⇒ AO = a
√
3
2
⇒ AC = a√3.
Suy ra diện tớch hỡnh thoi ABCD là SABCD =
1
2
AC.BD =
a2
√
3
2
.
Do đú thể tớch khối chúp S.ABCD là VS.ABCD =
1
3
SABCD.SA =
a3
√
3
6
.
A
B C
D
S
O
B′
D′K
C′
Gọi K = SO ∩ B′D′ ⇒ K là trọng tõm ∆SAC ⇒ SI
SO
=
2
3
.
Lại cú B′D′||BD ⇒ SB
′
SB
=
SD′
SD
=
2
3
.
Do đú
VS.AB′C′
VS.ABC
=
SA
SA
.
SB′
SB
.
SC′
SC
= 1.
2
3
.
1
2
=
1
3
⇒ VS.AB′C′ = 13VS.ABC =
1
6
VS.ABCD.
Tương tự
VS.AD′C′
VS.ADC
=
SA
SA
.
SD′
SD
.
SC′
SC
= 1.
2
3
.
1
2
=
1
3
⇒ VS.AD′C′ = 13VS.ADC =
1
6
VS.ABCD.
Vậy VS.AB′C′D′ = VS.AB′C′ +VS.AD′C′ =
1
3
VS.ABCD =
a3
√
3
18
.
Cõu 7 (1,0 điểm).
A
B C
E
N
M
H
d
Ta cú A ∈ d⇒ A(t; t+ 1); điểm M trung điểm AC ⇒ C(6− t; 1− t).
Khi đú
−→
HA = (t− 2; t+ 2),−→HC = (4− t; 2− t).
Điểm H là chõn đường cao kẻ từ A nờn
−→
HA.
−→
HC = 0⇔ t = 2⇒ A(2; 3),C(4;−1).
Ta cú
−→
EC = (9;−1)⇒ trung tuyến CE cú phương trỡnh x+ 9y+ 5 = 0.
Và
−→
HC = (2; 0)⇒ đường thẳng BC cú phương trỡnh y+ 1 = 0.
Gọi N là trung điểm AB, ta cú B ∈ BC ⇒ B(b;−1)⇒ N
ầ
b+ 2
2
; 1
ồ
.
Lại cú N ∈ CE nờn b+ 2
2
+ 9+ 5 = 0⇔ b = −30⇒ B (−30;−1).
Vậy B(−30;−1).
3
Cõu 8 (1,0 điểm).
Mặt phẳng (P) cú vectơ phỏp tuyến −−→n(P) = (2; 1;−1).
Mặt phẳng (Q) qua M(1;−2; 3) và nhận −−→n(P) = (2; 1;−1) làm một vectơ phỏp tuyến.
Do đú (Q) cú phương trỡnh 2(x− 1) + (y+ 2)− (z− 3) = 0⇔ 2x+ y− z+ 3 = 0.
Gọi H là hỡnh chiếu của M trờn (P)⇒ MH⊥(P).
Suy ra MH đi qua M(1;−2; 3) và nhận −−→n(P) = (2; 1;−1) làm một vectơ chỉ phương.
Do đú MH cú phương trỡnh

x = 1+ 2t
y = −2+ t
z = 3− t
⇒ H(1+ 2t;−2+ t; 3− t).
Mặt khỏc H ∈ (P) nờn 2(1+ 2t) + (−2+ t)− (3− t)− 6 = 0⇔ t = 3
2
⇒ H
ầ
4;−1
2
;
3
2
ồ
.
Vậy (Q) : 2x+ y− z+ 3 = 0 và H
ầ
4;−1
2
;
3
2
ồ
.
Cõu 9 (0,5 điểm).
Phộp thử là lấy mỗi hộp một vỉ thuốc nờn |Ω| = 10ì 10 = 100.
Gọi A là biến cố "lấy được hai vỉ hỏng", ta cú |ΩA| = 2ì 4 = 8.
Vậy xỏc suất của biến cố A là P(A) =
|ΩA|
|Ω| =
8
100
=
2
25
.
Cõu 10 (1,0 điểm).
Theo bất đẳng thức Cauchy− Schwarz và giả thiết ta cú :
(a+ b+ c)2 6 3
Ä
a2 + b2 + c2
ọ
= 36⇔ a+ b+ c 6 6
Lại theo bất đẳng thức AM− GM ta cú :Ä
b2 + c2
ọ
+ 2a2 + 4a > 6a 3
√
b2 + c2 (1)Ä
c2 + a2
ọ
+ 2b2 + 4b > 6b 3
√
c2 + a2 (2)Ä
a2 + b2
ọ
+ 2c2 + 4c > 6c 3
√
a2 + b2 (3)
Cộng theo vế (1), (2) và (3) được :
a 3
ằ
b2 + c2 + b 3
ằ
c2 + a2 + c 3
ằ
a2 + b2 6 4
Ä
a2 + b2 + c2
ọ
+ 4 (a+ b+ c)
6
6 12
Ta cú bất đẳng thức cần chứng minh.
———Hết ———
4