Đáp án đề kiếm tra chất lượng cuối kì i - Thạch Thành - Thanh Hóa năm học: 2015 - 2016 môn: Toán 7

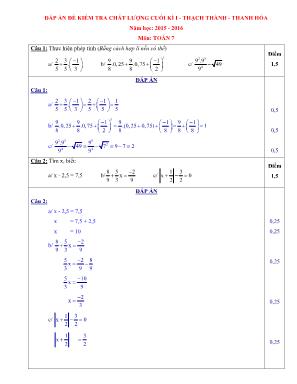
ĐÁP ÁN ĐỀ KIẾM TRA CHẤT LƯỢNG CUỐI KÌ I - THẠCH THÀNH - THANH HÓA 
Năm học: 2015 - 2016 
Môn: TOÁN 7 
Câu 1: Thực hiện phép tính (Bằng cách hợp lí nếu có thể) 
 a/ 
2 3 1
.
5 5 3
 
  
 
 b/ 
3
9 9 1
.0, 25 .0,75
8 8 2
 
   
 
 c/ 
2 3
4
9 .9
49
9
 
Điểm 
1,5 
ĐÁP ÁN 
Câu 1: 
 a/ 
2 3 1 2 1 1
.
5 5 3 5 5 5
    
      
   
 b/ 
3
9 9 1 9 1 9 1
.0, 25 .0,75 .(0,25 0,75) 1
8 8 2 8 8 8 8
       
            
     
 c/ 
2 3 5
2
4 4
9 .9 9
49 7 9 7 2
9 9
      
0,5 
0,5 
0,5 
Câu 2: Tìm x, biết: 
 a/ x - 2,5 = 7,5 b/
8 5 2
x
9 3 9

  c/ 
1 3
x 0
2 2
   
Điểm 
1,5 
ĐÁP ÁN 
Câu 2: 
 a/ x - 2,5 = 7,5 
 x = 7,5 + 2,5 
 x = 10 
 b/ 
8 5 2
x
9 3 9

  
5 2 8
x
3 9 9

  
5 10
x
3 9

 
2
x
3

 
 c/ 
1 3
x 0
2 2
   
1
x
2
 
3
2
 
0,25 
0,25 
0,25 
0,25 
0,25 
1 3
x
x 12 2
1 3 x 2
x
2 2

  
       

0,25 
Câu 3: Trong đợt thi đua dành nhiều điểm tốt chào mừng ngày Nhà giáo Việt Nam. Ba lớp 7A, 
7B, 7C đạt được số điểm tốt tỉ lệ với các số 8; 3; 5. Tính số điểm tốt đã đạt được của mỗi lớp, biết 
rằng cả ba lớp đạt được tất cả 256 điểm tốt. 
Điểm 
2,0 
ĐÁP ÁN 
Câu 3: 
 Gọi số điểm tốt đã đạt được của ba lớp 7A, 7B, 7C lần lượt là x, y, x (điểm) (x, y, z  N*, 
x, y, z < 256). 
 Vì cả ba lớp đạt tất cả 256 điểm tốt nên: 
 x + y + z = 256 
 Vì ba lớp 7A, 7B, 7C đạt được số điểm tốt tỉ lệ với các số 8; 3; 5 nên: 
x y z
8 3 5
  
 Áp dụng tính chất dãy tỉ số bằng nhau và x + y + z = 256, ta có: 
x y z x y z 256
16
8 3 5 8 3 5 16
 
    
 
x
16
8 x 8.16 128
y
16 y 3.16 48
3
z 5.16 80
z
16
5


 
 
     
   


 Vậy số điểm tốt đã đạt được của ba lớp 7A, 7B, 7C lần lượt là 128, 48, 80 (điểm) 
0,25 
0,25 
0,25 
0,25 
0,25 
0,5 
0,25 
Câu 4: Cho hàm số y = f(x) = 3x - 1 
 a/ Tính 
1
f
3
 
 
 
 b/ Biết điểm A(a, 2a) thuộc đồ thị hàm số y = 3x - 1. Tìm giá trị của a 
Điểm 
1,0 
ĐÁP ÁN 
Câu 4: 
 a/ Ta có: f(x) = 3x - 1 
1 1
f 3. 1 0
3 3
 
   
 
0,5 
AF
CB
D
E
 Vậy 
1
f 0
3
 
 
 
 b/ Vì điểm A(a, 2a) thuộc đồ thị hàm số y = 3x - 1 nên 
 2a = 3a - 1 
 a = 1 
 Vậy a = 1 
0,25 
0,25 
Câu 5: Cho tam giác ABC (AB < AC), tia phân giác của góc A cắt cạnh BC tại D. Trên cạnh AC 
lấy điểm E sao cho AE = AB. Trên tia đối của tia DE lấy điểm F sao cho DF = DC. Chứng minh 
rằng: 
 a/ ABD = AED 
 b/ BF = EC 
 c/ Ba điểm A, B, F thẳng hàng. 
Điểm 
3,0 
ĐÁP ÁN 
Câu 5: 
GT 
 ABC (AB < AC),  BAD CAD 
AB = AE, DF = DC. 
KL 
a/ABD = AED 
b/ BF = EC 
c/ A, B, F thẳng hàng 
a/ XétABD và AED có: 
 AB = AE (GT) 
  BAD CAD (GT) 
 AD: Cạnh chung 
 ABD = AED (c - g - c) 
b/ Ta có: ABD = AED (Theo câu a) 
 BD = ED (Hai cạnh tương ứng) 
XétBDF và EDC có: 
 BD = ED (Chứng minh trên) 
  BDF EDC (Hai góc đối đỉnh) 
 DF = DC (GT) 
 BDF = EDC (c - g - c) 
 BF = EC (Hai cạnh tương ứng) 
c/ Ta có: 
0,5 
0,25 
0,25 
0,25 
0,25 
0,25 
0,5 
0,25 
ABD = AED (Theo câu a) 
 ABD AED (Hai góc tương ứng) (1) 
BDF = EDC (Theo câu b) 
 DBF DEC (Hai góc tương ứng) (2) 
Từ (1), (2) và AED + DEC = 1800 ABD + DBF = 1800 hay ABD và DBF là hai góc kề bù 
 Ba điểm A, B, F thẳng hàng. 
0,25 
0,25 
Câu 6: Cho A = 
2 3 4 99 100
3 3 3 3 3 3
1 ...
4 4 4 4 4 4
         
               
         
 Chứng tỏ rằng A không phải là số nguyên 
Điểm 
1,0 
ĐÁP ÁN 
Câu 6: Ta có: 
 A = 
2 3 4 99 100
3 3 3 3 3 3
1 ...
4 4 4 4 4 4
         
               
         
3
4
 A = 
2 3 4 5 100 101
3 3 3 3 3 3 3
...
4 4 4 4 4 4 4
           
                 
           
  A + 
3
4
 A = 
2 3 4 99 100
3 3 3 3 3 3
1 ...
4 4 4 4 4 4
         
               
     
 
 
    

 + 
 + 
2 3 4 5 100 101
3 3 3 3 3 3 3
...
4 4 4 4 4 4 4
            
                               
  
7
A
4
 = 1 + 
101
3
4
 
 
 
100101 101 101 101
101 100
7 4 3 4 3 4 3 3
A A
4 4 7.4 7 7 4
   
       
 
Vì 
100 100
3 3 3 3
1 .
4 7 4 7
   
      
   
100
4 3 3 4 3
A 1
7 7 4 7 7
 
     
 
 hay 0 < A < 1 
 Vậy A không phải là số nguyên 
0,25 
0,5 
0,25