Chuyên đề luyện thi THPT Quốc gia môn Toán - Chuyên đề: Thể tích khối đa diện có yếu tố góc

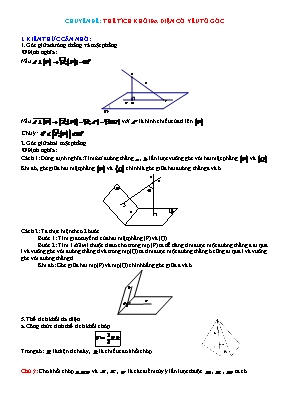
CHUYÊN ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN CÓ YẾU TỐ GÓC
I. KIẾN THỨC CẦN NHỚ: 
1. Góc giữa đường thẳng và mặt phẳng
µ Định nghĩa:
Nếu 
Nếu với là hình chiếu của d lên 
 Chú ý: 
2. Góc giữa hai mặt phẳng
µ Định nghĩa:
Cách 1: Dùng định nghĩa: Tìm hai đường thẳng , lần lượt vuông góc với hai mặt phẳng và . Khi đó, góc giữa hai mặt phẳng và chính là góc giữa hai đường thẳng a và b
Cách 2: Ta thực hiện theo 2 bước
	Bước 1: Tìm giao tuyến d của hai mặt phẳng (P) và (Q). 
	Bước 2: Tìm 1 điểm I thuộc d sao cho trong mp (P) ta dễ dàng tìm được một đường thẳng a đi qua I và vuông góc với đường thẳng d và trong mp(Q) ta tìm được một đường thẳng b cũng đi qua I và vuông góc với đường thẳng d. 
	Khi đó: Góc giữa hai mp(P) và mp(Q) chính bằng góc giữa a và b
5. Thể tích khối đa diện
a. Công thức tính thể tích khối chóp
Trong đó: là diện tích đáy, là chiều cao khối chóp.
Chú ý: Cho khối chóp và , , là các điểm tùy ý lần lượt thuộc , , ta có
 	.
b. Công thức thể tích khối lăng trụ : (là diện tích đáy, là chiều cao)
XÁC ĐỊNH CHIỀU CAO THƯỜNG GẶP
a) Hình chóp có một cạnh bên vuông góc với đáy: Chiều cao của hình chóp là độ dài cạnh bên vuông góc với đáy.
Ví dụ: Hình chóp có cạnh bên vuông góc với mặt phẳng đáy, tức thì chiều cao của hình chóp là 
b) Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam giác chứa trong mặt bên vuông góc với đáy.
Ví dụ: Hình chóp có mặt bên vuông góc với mặt phẳng đáy thì chiều cao của hình chóp là là chiều cao của 
c) Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai mặt bên cùng vuông góc với mặt phẳng đáy.
Ví dụ: Hình chóp có hai mặt bên và cùng vuông góc với mặt đáy thì chiều cao của hình chóp là 
d) Hình chóp đều:
Chiều cao của hình chóp là đoạn thẳng nối đỉnh và tâm của đáy. Đối với hình chóp đều đáy là tam giác thì tâm là trọng tâm G của tam giác đều.
Ví dụ: Hình chóp đều có tâm đa giác đáy là giao điểm của hai đường chéo hình vuông thì có đường cao là 
XÁC ĐỊNH DIỆN TÍCH ĐÁY HAY GẶP
1. Diện tích tam giác vuông.
·S= nửa tích 2 cạnh góc vuông.
· Pitago: 
2. Diện tích tam giác đều.
· S= (cạnh)2.34 
· h= (cạnh).32
3. Diện tích hình vuông: 
·. S= (cạnh)2
·. Pitago: 
·.Đường chéo hình vuông bằng cạnh.
4. Diện tích hình chữ nhật: 
·. S= dài x rộng.
5. Diện tích hình thoi: 
·. 
·. S= 2.SABC=2.SADC
6. Diện tích hình thang: 
·. S= nửa chiều cao x (đáy lớn+bé) 
·. 
II. CÁC DẠNG BÀI TẬP TƯƠNG TỰ
Ÿ Thể tích khối đa diện
Ÿ Góc giữa đường thẳng và mặt phẳng
Ÿ Góc giữa hai mặt phẳng
Ÿ Công thức tỉ số thể tích
Ÿ Khoảng cách từ 1 điểm tới mặt phẳng
Ÿ Khoảng cách giữa hai đường thẳng chéo nhau
BÀI TẬP MẪU
(ĐỀ MINH HỌA-BDG 2020-2021) Cho hình chóp có đáy là tam giác đều cạnh , cạnh bên vuông góc với đáy, góc giữa và mặt phẳng bằng ( tham khảo hình bên). Thể tích của khối chóp bằng:
A. .	B. .	C. .	D. .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tính thể tích biết chiều cao khối đa diện biết góc giữa mặt bên và mặt đáy.
2. HƯỚNG GIẢI: 
B1: Tính diện tích đáy
B2: tính thể tích khối lăng trụ 
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn A 
Gọi là trung điểm thì và nên . 
Từ đây dễ thấy góc cần tìm là .
Do đó tam giác vuông cân tại và .
Suy ra 
Bài tập tương tự và phát triển:
Ä Mức độ 1
Cho hình chóp có diện tích mặt đáy là và chiều cao bằng . Thể tích của khối chóp bằng
A. .	B. .	C. .	D. .
 Lời giải
Chọn B
Ta có .
Thể tích của khối chóp có chiều cao bằng và diện tích đáy bằng là
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Ta có .
Khi tăng độ dài các cạnh của một khối chóp lên lần thì thể tích của khối chóp thay đổi như thà nào?
A. Tăng lần. .	B. Tăng lần..	C. Tăng lần.	D. Không thay đổi.
Lời giải
Chọn B
Thể tích khối chóp là: .
Độ dài cạnh đáy tăng lên lần thì diện tích mặt đáy tăng lần.
Cạnh bên tăng lên lần thì chiều cao của hình chóp tăng lên lần.
Vậy khi tăng độ dài các cạnh của một khối chóp lên lần thì thể tích của khối chóp tăng lên lần.
Công thức tính thể tích của khối chóp có diện tích đáy và chiều cao là
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Công thức tính thể tích của khối chóp có diện tích đáy và chiều cao là .
Khối chóp có , , , cố định và chạy trên đường thẳng song song với . Khi đó thể tích khối chóp sẽ:
A. Giảm phân nửa..	B. Tăng gấp đôi..	C. Tăng gấp bốn.	D. Giữ nguyên..
Lời giải.
Chọn D
Gọi là đường thẳng qua và song song .
Ta có: 
+ song songnên không đổi.
+, , , cố định nên diện tích tứ giác cũng không đổi.
Vì vậy thể tích khối chóp sẽ giữ nguyên.
Cho khối chóp có thể tích là , đáy là hình vuông cạnh . Độ dài chiều cao khối chóp bằng.
A. .	B. .	C. .	D. .
Lời giải
Chọn A
.
Cho hình chóp có đáy là hình vuông cạnh và thể tích bằng .Tính chiều cao của hình chóp đã cho.
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Ta có:.
Cho hình chóp có đáy là tam giác đều cạnh và thể tích bằng . Tính chiều cao của hình chóp đã cho.
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Do đáy là tam giác đều nên .
Mà .
Nếu độ dài chiều cao của khối chóp tăng lên lần, diện tích đáy không đổi thì thể tích của khối chóp sẽ tăng lên
A. lần.	B. lần.	C. lần.	D. lần.
Lời giải
Chọn A
Thể tích khối chóp sẽ tăng lên lần.
Cho hình chóp có đáy là tam giác đều cạnh và chiều cao . Tính thể tích của hình chóp đã cho.
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Do đáy là tam giác đều nên .
Mà .
Cho hình chóp tam giác có đáy là tam giác vuông tại , ,, cạnh bên vuông góc với mặt đáy và . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Diện tích đáy 
Chiều cao: 
Cho hình chóp tam giác có đáy là tam giác đều cạnh , cạnh bên vuông góc với mặt đáy và . Tính thể tích của khối chóp.
A. 	B. 	C. 	D. .
Lời giải
Chọn B
Diện tích đáy 
Chiều cao: 
Cho khối chóp có vuông góc với , đáy là tam giác vuông cân tại , , góc giữa và là . Tính thể tích khối chóp . 
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có là hình chiếu của lên suy ra góc giữa và là góc .
Tam giác vuông cân tại , .
Xét vuông tại có .
Ta có . Vậy .
Cho khối chóp có đáy là hình chữ nhật,, , vuông góc với mặt phẳng đáy và mặt phẳng tạo với đáy một góc . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Ta có .
Dễ thấy .
Xét tam giác vuông có: 
Vậy .
Cho hình chóp có và vuông góc với đáy . Biết rằng tam giác đều và mặt phẳng hợp với đáy một góc . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. .
Lời giải:
Chọn A 
Gọi là trung điểm ta có 
Xét tam giác vuông tại ta có 
Ta có 
Diện tích 
Thể tích 
Cho khối chóp có vuông góc với , đáy là tam giác vuông cân tại , , góc giữa và là . Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải:
Chọn A
 là hình chiếu của lên suy ra góc giữa và là góc .
 Tam giác vuông cân tại , .
.
 .
 .
Cho hình chóp có đáy là tam giác đều cạnh , tam giác là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải:
Chọn B
Gọi là trung điểm của .
, .
. 
Cho hình chóp có đáy là hình chữ nhật. Tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết và góc tạo bởi đường thẳng và mặt phẳng bằng . Tính thể tích của khối chóp .
A. .	B. .	C. 	D. 
Lời giải
Chọn D.
Ta có , , .
. 
Từ đó: 
Vậy .
Cho hình chóp có đáy là hình thang vuông tại và , , . Hình chiếu của lên mặt phẳng trùng với trung điểm cạnh . Biết rằng. Tính theo thể tích của khối chóp .
A. 	B. .	C. .	D. .
Lời giải
Chọn C. 
Gọi là trung điểm . Ta có: suy ra .
Nên .
Cho khối chóp tam giác đều có cạnh đáy bằng và cạnh bên bằng . Tính thể tích của khối chóp 
A. .	B. .	C. .	D. .
Lời giải
Chọn B.
Do đáy là tam giác đều nên gọi là trung điểm cạnh , khi đó là đường cao của tam giác đáy. Theo định lý Pitago ta có , và .
Trong tam giác vuông tại ta có 
Vậy thể tích khối chóp là .
Ä Mức độ 2
Cho khối chóp có đáy là hình vuông cạnh , vuông góc với đáy và tạo với mặt phẳng một góc Tính thể tích của khối chóp đã cho.
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có 
Suy ra 
Thể tích khối chóp : . 
Cho hình chóp có đáy là hình chữ nhật , , , vuông góc với mặt phẳng . Tính thể tích khối chóp tính theo .
A. 	B. 	C. 	D. 
Lời giải
Chọn B
Ta có .
Thể tích khối chóp là .
Cho hình chóp có đáy là tam giác vuông tại , , . Cạnh bên và vuông góc với mặt phẳng . Tính thể tích khối chóp . 
A. 	B. 	C. 	D. 
Lời giải
Chọn B. 
Vì tam giác vuông tại nên 
 (đvtt).	.
Cho hình chóp có đáy là hình chữ nhật, , , đường thẳng vuông góc với mặt phẳng và . Thể tích của khối chóp bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Áp dụng công thức tính thể tích khối chóp ta có .
Cho hình chóp có cạnh bên vuông góc với mặt phẳng đáy . Biết , tam giác là tam giác vuông cân tại , . Tính theo thể tích của khối chóp .
A. 	B. 	C. 	D. 
Lời giải
Chọn D
Ta có: (dvtt). 
Cho khối chóp tam giác có , tam giác có độ dài cạnh là ; ; , góc giữa và là . Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn B 
Ta có nửa chu vi là .
Diện tích là .
 nên vuông, cân tại nên .
Thể tích khối chóp là .
Cho hình chóp có mặt phẳng vuông góc với mặt phẳng , là tam giác đều cạnh , đường thẳng tạo với mặt phẳng góc . Thể tích của khối chóp bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Ta thấy tam giác cân tại , gọi là trung điểm của suy ra 
Do nên .
Ta lại có nên thuộc trục đường tròn ngoại tiếp tam giác là tâm đường tròn ngoại tiếp tam giác .
Do là hình chiếu của lên mặt phẳng .
Ta có , .
.
Cho hình chóp có đáy là hình vuông cạnh , cạnh vuông góc với đáy và mặt phẳng tạo với đáy một góc . Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn C	
Ta có: mà .
Ta có: . Vậy .
Cho hình chóp có đáy là hình vuông cạnh , hai mặt phẳng và cùng vuông góc với mặt phẳng ; góc giữa đường thẳng và mặt phẳng bằng . Tính theo thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Ta có 
 là hình chiếu vuông góc của lên mặt phẳng 
Tam giác vuông tại có .
Khi đó .
Cho hình chóp có đáy là hình chữ nhật với , . Cạnh bên vuông góc với đáy và đường thẳng tạo với mặt phẳng một góc . Tính thể tích của khối chóp theo .
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có: là hình chiếu của lên mặt phẳng .
.
Xét tam giác vuông tại có .
Xét tam giác vuông tại có .
Mà .
Vậy .
Cho hình chóp tứ giác đều có cạnh đáy bằng và cạnh bên tạo với mặt phẳng đáy một góc . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. 
Lời giải
Chọn.D.
Ta có: .
Chiều cao : .
Vậy .
Cho hình chóp tứ giác đều có cạnh đáy bằng và mặt bên tạo với mặt phẳng đáy một góc . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. 
Lời giải
Chọn D.
Ta có: .
Gọi là trung điểm , góc giữa mặt bên và là 
Ta có 
Chiều cao : .
Vậy .
Cho lăng trụ đứng có đáy là tam giác cân tại , , , góc giữa và là . Tính thể tích lăng trụ đã cho. 
A. .	B. .	C. .	D. 
Lời giải
Chọn D.
Gọi là trung điểm của . Ta có và ( docân tại )
Ta xác định được góc giữa và là 
Ta có và
; 
	Vậy (đơn vị thể tích).
Cho hình chóp tam giác đều có cạnh đáy bằng và cạnh bên tạo đáy góc . Thể tích của khối chóp đó bằng:
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có: . Gọi là trọng tâm của tam giác , suy ra .
Ta có là hình chiếu của lên mặt phẳng .
Suy ra . Xét tam giác vuông tại , ta có:
.
Vậy .
Cho hình lăng trụ đều . Mặt phẳng tạo với mặt phẳng một góc và tam giác có diện tích bằng . Tính thể tích khối lăng trụ .
A. .	B. .	C. .	D. .
Lời giải
Chọn B.
Kẻ đường cao của tam giác . Khi đó là trung điểm của 
Tam giác vuông tại nên góc là góc nhọn.
Góc giữa hai mặt phẳng và bằng góc giữa và và bằng góc , bằng 
Tam giác là hình chiếu vuông góc của tam giác trên 
Suy ra .
Đặt . Diện tích tam giác đều theo là .
Vậy có 
Tam giác vuông tại , .
	Thể tích của lăng trụ là .
Cho hình hộp chữ nhật có đáy là hình vuông, cạnh bên bằng và đường chéo .Tính thể tích hình hộp chữ nhật này.
A. .	B. .	C. .	D. .
Lời giải
Chọn B.
ABCD là hình vuôngÞ 
	Vậy 
Cho hình chóp có đáy là tam giác vuông tại , , . Hình chiếu vuông góc của lên là trung điểm của . Góc giữa và đáy bằng . Thể tích là bao nhiêu?
A. .	B. .	C. .	D. .
Lời giải
Chọn B.
Diện tích ABC : 
Thể tích S.ABC : .
Cho hình chóp có đáy là hình chữ nhật với , . Hình chiếu của lên mặt phẳng là trung điểm của cạnh , đường thẳng tạo với đáy một góc. Tính thể tích của khối chóp .
A. .	B. .	C. .	D. 
Lời giải
Chọn A.
Ta có .
Do tạo với đáy một góc nên .
Mà . Vậy .
Cho khối chóp có đáy là hình vuông cạnh , cân tại và nằm trong mặt phẳng vuông góc với đáy. Góc giữa và mặt đáy bằng . Tính thể tích bằng:
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Gọi là trung điểm . 
Ta có: .
 là hình vuông cạnh nên.
Tam giác cân tại , mà góc giữa mặt phẳng và mặt phẳng là góc giữa hai đường thẳng , chính là góc . Theo bài ra có .
.
Vậy thể tích : .
Cho hình chóp tam giác đều có cạnh đáy bằng , cạnh bên bằng . Tính thể tích của khối chóp .
A. .	B. . 	C. .	D. .
Lời giải
Chọn D
Diện tích đáy ; 
Chiều cao: 
Ä Mức độ 3
Cho hình chóp có đáy là hình vuông cạnh , , . Gọi là trọng tâm tam giác . Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Gọi lần lượt là trung điểm của và .
Ta có .
Ta có .
Cho hình chóp có đáy là tam giác vuông tại , , . Tam giác cân tại và nằm trong mặt phẳng vuông góc với đáy. Gọi là trọng tâm tam giác , mặt phẳng tạo với đáy một góc . Thể tích khối tứ diện bằng
A. 	B. 	C. 	D. 
Lời giải
Chọn A
Ta có: .
Gọi là trung điểm của .
Gọi là trung điểm của , là trung điểm của và là trung điểm của .
Ta có .
Do nên góc giữa và đáy là .
Ta có: , .
Vậy .
Cho hình chóp có tam giác vuông cân tại , mặt phẳng vuông góc với mặt đáy. Các mặt bên , tạo với mặt đáy các góc bằng nhau và bằng . Tính theo thể tích của khối chóp .
A. 	B. 	C. 	D. 
Lời giải
Chọn D
Ta có: và .
Trong mặt phẳng , kẻ thì .
Gọi , lần lượt là hình chiếu vuông góc của lên cạnh và thì và .
Mà nên tứ giác là hình vuông là trung điểm cạnh .
Khi đó tứ giác là hình vuông cạnh và .
Vậy .
Hình chóp có đáy là hình vuông cạnh là tam giác cân tại và nằm trong mặt phẳng vuông góc với đáy . Biết côsin của góc tạo bởi mặt phẳng và bằng . Thể tích của khối chóp là
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Gọi là trung điểm , là trung điểm 
Ta có . 
Vậy .
Cho hình chóp với đáy là hình thang vuông tại và , đáy nhỏ của hình thang là , cạnh bên . Tam giác là tam giác đều cạnh và nằm trong mặt phẳng vuông góc với đáy hình chóp. Gọi là trung điểm cạnh , khoảng cách từ tới mặt phẳng bằng . Tính thể tích của khối chóp ?
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Ta có , .
.
Ta có nên .
Đặt nên ; 
.
.
.
 Vậy .
Cho hình chóp có đáy là hình thang vuông tại và ; biết Góc giữa hai mặt phẳng và bằng Gọi là trung điểm của , biết hai mặt phẳng và cùng vuông góc với mặt phẳng . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn B
.
Như đã nhắc ở Câu trước thì do hai mặt phẳng và cùng vuông góc với nên nên là đường cao của .
Kẻ tại . Khi đó ta chứng minh được . Ta vẽ hình phẳng của mặt đáy. Ta có ta chứng minh được là đường tủng bình của tam giác Khi đó . Ta có .
Khi đó . .
Cho hình chóp có đáy là hình vuông tâm , mặt bên là tam giác vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của khối chóp bằng . Tính khoảng cách từ đến mặt phẳng ?
A. .	B. .	C. .	D. .
Lời giải
Chọn A
.
Gọi là độ dài ,kẻ tại , ta có .
Do là trung điểm của nên khoảng cách từ đến mặt phẳng gấp lần khoảng cách từ đến mặt phẳng mà .
Tính : kẽ , ta chứng minh được , , vậy .
Cho hình chóp có đáy là hình thang vuông tại và , . Tam giác đều và nằm trong mặt phẳng vuông góc với đáy, góc giữa và mặt phẳng bằng sao cho . Tính thể tích khối chóp theo .
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Gọi là trung điểm , từ giả thiết ta có: , .
Đặt , ta có: , .
Mặt khác . Vậy ta có: .
; ; .
Cho hình chóp có đáy là hình chữ nhật; . Tam giác cân tại và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng và mp bằng . Gọi là trung điểm của . Tính theo khoảng cách từ điểm đến .
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Gọi là trung điểm đoạn.
Xét vuông tại , có: .
Xét vuông cân tại , có: .
Xét vuông tại , có: .
Xét vuông tại , có: .
.
Ta có: ; .
. Mà .
Cho hình chóp có đáy là hình chữ nhật, tam giác vuông tại và nằm trong mặt phẳng vuông góc với đáy. Cho biết , . Mặt phẳng tạo với đáy một góc . Thể tích khối chóp là
A. 	B. 	C. 	D. 
Lời giải
Chọn B
Gọi là hình chiếu của lên cạnh , là hình chiếu của lên cạnh , ta có
 và . Suy ra .
Trong tam giác vuông đặt nên từ ta có .
Do đó . Suy ra .
Thể tích khối chóp là .
Cho hình chóp có đáy là hình chữ nhật, mặt bên là tam giác vuông tại . Hình chiếu vuông góc của trên mặt phẳng đáy là điểm thuộc cạnh sao cho . Biết rằng và tạo với đáy một góc bằng . Tính theo thể tích của khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Có: .
.
Tam giác có .
Tam giác có 
Vậy .
Cho hình chóp có đáy là tam giác đều cạnh , . Gọi là trung điểm của . Biết khoảng cách từ đến bằng . Thể tích của khối chóp đã cho bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Trong mp xác định điểm sao cho tứ giác vuông tại và 
Khi đó ta có: ; 
Vậy 
Có tam giác là tam giác đều cạnh 
Ta đi tìm 
Gọi là trung điểm 
vì tam giác đều, nội tiếp đường tròn đường kính Þ 
Gọi là trọng tâm tam giác và là trung điểm 
Vì tam giác đều , tương tự 
Dễ thấy là hình thoi 
Xét hình chóp có đáy là hình thang vuông tại C, N. 
Khoảng cách từ đến mặt phẳng bằng vì .
Trong mp gọi 
Trong mp kẻ tia gọi 
Gọi K là hình chiếu của G trên mặt phẳng 
Khi đó ta có 
Trong mp kẻ ta có 
Mà tam giác là tam giác đều cạnh 
Từ 
Dễ thấy 
Xét tam giác có nên (theo )
Xét tam giác có nên 
Từ và ta có 
Vậy .
Cho hình chóp biết rằng , , và . Thể tích khối chóp là
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có , suy ra tam giác đều .
Lại có , suy ra tam giác vuông cân tại .
Mặt khác, , , áp dụng định lí cosin cho tam giác , ta được:
.
Xét tam giác có suy ra tam giác vuông tại .
Vậy diện tích tam giác là: .
Gọi là trung điểm của cạnh suy ra là tâm đường tròn ngoại tiếp tam giác .
Mà .
Xét tam giác vuông vuông tại có .
Vậy thể tích khối chóp là: .
Cho hình chóp có . Các mặt bên tạo với đáy góc . Tính thể tích khối chóp . Biết hình chiếu vuông góc của trên thuộc miền trong của tam giác .
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Ta có .
Diện tích tam giác là 
Gọi là hình chiếu vuông góc của trên .
Gọi là hình chiếu vuông góc của trên , .
Theo bài ra ta có .
Ta có vì
,
chung,
.
Suy ra .
Vậy là tâm đường tròn nội tiếp tam giác .
Khi đó .
.
Thể tích khối chóp là .
Cho hình chóp có , ,, . Tính thể tích khối chóp 
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Gọi là trung điểm của cạnh . Vì cân tại (do ) nên . ; .
 nên . Gọi là hình chiếu vuông góc của điểm trên mặt phẳng suy ra .
Áp dụng định lí cosin cho , ta có: .
 vuông tại nên .
Áp dụng định lí cosin cho , ta có .
.
.
Vậy .
Cách 2:
Áp dụng định lí cosin cho , ta có
.
Sử dụng công thức 
.
Cho hình chóp có đáy là hình thoi cạnh , , gọi I là giao điểm và . Hình chiếu vuông góc của S lên mặt phẳng là sao cho là trung điểm của . Góc giữa và bằng . Tính thể tích của khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Tam giác đều cạnh 
Áp dụng định lí cosin cho tam giác 
Xét tam giác vuông tại : 
Do tam giác vuông tại , có nên tam giác vuông cân tại . Suy ra: 
Vậy thể tích khối chóp : 
Cho hình chóp có đáy là tam giác đều cạnh , khoảng cách từ điểm đến mặt phẳng là , khoảng cách giữa và là . Biết hình chiếu của lên mặt phẳng nằm trong tam giác , tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Dựng hình bình hành . Gọi là hình chiếu vuông góc của lên mặt phẳng .
Dựng đường thẳng đi qua , vuông góc với và cắt lần lượt tại .
Khi đó .
Trong , dựng và .
Ta có và nên .
Vì vậy .
Do nên . Suy ra .
Do có hai đường cao nên cân tại . Suy ra là trung điểm của .
Ta có (do đều, cạnh bằng ). Suy ra .
Xét hai tam giác đồng dạng và , ta có
.
Vậy thể tích khối chóp là .
Cho hình lăng trụ đứng có đáy là tam giác vuông cân tại , cạnh . Góc giữa mặt phẳng và mặt phẳng bằng . Tính thể tích khối đa diện .
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Chọn D
Gọi là trung điểm , ta có và (trung tuyến trong tam giác vuông bằng nửa cạnh huyền).
Kẻ mà suy ra 
Vậy góc giữa mặt phẳng và mặt phẳng là .
Ta có ; 
Mặt khác .
Cho hình chóp có là hình thoi cạnh và . Biết rằng , và . là trọng tâm tam giác . Tính thể tích của tứ diện .
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Chọn B
Ta có .
* Tính ?
Gọi , do .
Kẻ , do nên .
Suy ra .
Do và là trung tuyến nên tam giác vuông cân tại .
Khi đó và .
Mà tam giác vuông tại có đường cao nên .
Vậy .
* Tính ?
Gọi là trung điểm của thì .
Gọi là trung điểm của thì .
Suy ra .
Vậy .
Cho hình chóp có đáy là hình vuông cạnh , và vuông góc với đáy. Gọi là trung điểm , là điểm thuộc cạnh sao cho . Tính thể tích của khối tứ diện .
	A. .	B. .	C. .	D. 
Hướng dẫn giải
Chọn D
Cách 1. Ta có 
Suy ra .
Mặt khác 
Vậy .
Cách 2. Gọi là giao điểm của và .
Ta có . Vì nên .
Do đó 
.
Cho lăng trụ là lăng trụ đứng, góc bằng . Góc giữa đường thẳng và mặt phẳng bằng . Tính thể tích lăng trụ đã cho.
A. .	B. .	C. .	D. .
Lời giải
Chọn B.
Kẻ . Vì lăng trụ là lăng trụ đứng nên . Do đó .
Góc giữa và bằng góc và bằng (tam giác vuông tại nên góc nhọn)
Xét tam giác , áp dụng định lý cosin cho cạnh có: 
.
.
Mặt khác 
Do đó 
Xét tam giác vuông tại nên 
Xét tam giác vuông tại nên 
	Thể tích của lăng trụ là .
Cho hình chóp có đáy là tam giác vuông tại. Biết vuông góc với mặt phẳng, . Một mặt phẳng qua vuông góc tại và cắt tại. Tính thể tích khối chóp theo.
A. .	B. .	C. .	D. .
Lời giải
Chọn B.
Ta có , suy ra 
Vì vuông cân tại nên là trung điểm của. Ta có:
. Ta có 
, khi đó 
, lại có 
	Vậy .
Cho hình chóp có đáy là tam giác vuông cân đỉnh . Hình chiếu vuông góc của lên mặt phẳng là trung điểm của . Mặt phẳng hợp với mặt phẳng đáy một góc bằng . Tính thể tích khối chóp .
A. 	B. 	C. 	D. 
Lời giải
Chọn D. 
Góc giữa mặt phẳng và mặt phẳng đáy là góc .
 có .
Do đó 
Cho hình chóp có đáy là tam giác vuông cân tại , có ; Mặt bên vuông góc với đáy, các mặt bên còn lại đều tạo với mặt đáy một góc 450. Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Gọi là hình chiếu vuông góc của lên cạnh nên .
Gọi , lần lượt là hình chiếu vuông góc của lên cạnh và . Khi đó, góc tạo bởi hai mặt phẳng , tạo với đáy lần lượt là , cùng bằng .
Hai tam giác , có , , nên hai tam giác bằng nhau hay . Mà là tam giác vuông cân nên là trung điểm của .
Ta có: . Vậy .
Cho hình chóp có đáy là hình chữ nhật, mặt bên là tam giác đều cạnh và nằm trong mặt phẳng vuông góc với mặt phẳng . Góc giữa mặt phẳng và mặt phẳng là . Thể tích của khối chóp là: 
A. .	B. .	C. .	D. .
Lời giải
Chọn A
+) Gọi lần lượt là trung điểm của (vì đều).
Gọi là trung điểm của (vì và vuông góc với nhau).
Suy ra 
 +) Tam giác cân tại , mà góc giữa mặt phẳng và mặt phẳng là góc giữa hai đường thẳng chính là góc . Theo bài ra có .
+) Vì là tam giác đều cạnh nên ta có .
. Vậy thể tích của của khối chóp là 
.
Cho hình chóp có đáy là tam giác vuông tại , , . Hình chiếu của điểm trên mặt phẳng trùng với trung điểm của đoạn thẳng . Biết rằng góc giữa mặt phẳng và mặt phẳng bằng . Thể tích của khối chóp là
A. .	B. .	C. .	D. .
Lời giải
Chọn D
, kẻ và , 
suy ra . 
Đặt , ta tính được và . 
Vậy , 
Tam giác vuông tại có 
Vậy .
Cho hình chóp có , , và , , . Khi đó thể tích khối chóp là
A. . 	B. .	C. .	D. .
Lời giải
Chọn B
Lấy là trung điểm của và lấy sao cho . Ta có nên hình chiếu vuông góc của lên trùng với tâm của đường tròn ngoại tiếp tam giác . 
Ta có: vì tam giác đều (cân tại và có một góc bằng ) 
 vì là cạnh huyền của tam giác vuông có cạnh góc vuông bằng 1.
Dễ đánh giá được tam giác vuông tại nên có 
Suy ra 
Suy ra 
	Áp dụng công thức tỉ số thể tích ta có suy ra 
Cho tứ diện có và . Gọi , lần lượt là trung điểm của và . Biết và là đoạn vuông góc chung của và . Tính thể tích tứ diện . 
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Dựng hình hộp chữ nhật chứa tứ diện như hình vẽ.
Ta có: 
Vậy .
Cho hình chóp tam giác có là trung điểm , là điểm trên sao cho , là điểm trên sao cho . Kí hiệu , lần lượt là thể tích khối chóp và . Tính tỉ số .
A. .	B. .	C. .	D. .
Lời giải.
Chọn A 
Ta có ;
Suy ra ; .
Cho hình chóp đều Gọi là trung điểm là điểm đối xứng với qua Mặt phẳng chia khối chóp thành hai phần có thể tích lần lượt là với Tính tỉ số 
A. .	B. .	C. .	D. 
Lời giải
Chọn A
F
E
M
N
S
A
C
B
D
Gọi lần lượt là chiều cao và diện tích đáy của khối chóp . Khi đó Nối cắt tại , cắt tại Tam giác có lần lượt là trung điểm của và suy ra là trọng tâm tam giác Tứ giác là hình bình hành nên là trung điểm 
Ta có 
= 
= 
Do đó 
Suy ra 
Ä Mức độ 4
Cho hình chóp có đáy là tam giác đều cạnh , biết khoảng cách từ đến là , từ đến là , từ đến là và hình chiếu vuông góc của xuống đáy nằm trong tam giác . Tính thể tích khối chóp .
A. 	B. 	C. 	D. 
Lời giải
Chọn B
Gọi lần lượt là hình chiếu của lên các cạnh .
Đặt .
Ta có 
Tương tự, tính được 
Ta có 
Vậy .
 [2H1-0.0-4] Cho hình chóp có đáy là hình vuông cạnh . Tam giác vuông tại và nằm trong mặt phẳng vuông góc với đáy. Gọi là góc tạo bởi đường thẳng và mặt phẳng , với . Tìm giá trị lớn nhất của thể tích khối chóp .
A. 	B. 	C. 	D. 
Lời giải
Chọn C
Gọi là đỉnh thứ tư của hình bình hành .
Khi đó mà (vì , ) nên là hình chiếu vuông góc của lên .
Góc giữa và là , do đó .
Đặt , .
Gọi là hình chiếu của lên , theo đề ta có .
Do đó đạt giá trị lớn nhất khi lớn nhất. Vì tam giác vuông tại nên 
Từ đó khi .
Suy ra .
Xét tứ diện có các cạnh và , thay đổi. Giá trị lớn nhất của thể tích tứ diện bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn B
Gọi , lần lượt là trung điểm và .
Theo giả thiết ta có: và là các tam giác cân có là trung điểm của nên và . Và có cân tại.
Trong tam giác có vừa là đường cao vừa là trung tuyến nên 
.
Khi đó diện tích tam giác là: 
Thể tích tứ diện là: .
Đặt , ta có: .
Ta có: .
Do đó: . Dấu bằng xảy ra khi .
Ta lại có: .
Dấu bằng xảy ra khi .
Vậy giá trị lớn nhất của thể tích tứ diện là: tập xác định .
Cho hình chóp tam giác đều có cạnh đáy bằng . Gọi lần lượt là trung điểm của Tính thể tích khối chóp . Biết mặt phẳng vuông góc với mặt phẳng .
A. .	B. .	C. .	D. .
Lời giải
Chọn B
 là trung điểm nên 
.
SE vừa là trung tuyến vừa là đường cao nên cân tại 
 là giao điểm của với .
Giả thiết 
 và nên cân tại 
.
.
Vậy .
Cho hình chóp có , và khoảng cách từ đến mặt phẳng bằng . Tính thể tích khối . 
	A. .	B. .	C. .	D. .
Lời giải
Chọn B
Hạ tại có
. 
Chứng minh tương tự có .
Hai tam giác vuông và bằng nhau suy ra .
Gọi là trung điểm của suy ra tứ giác là hình thoi và . 
Gọi là tâm hình thoi có . 
.
Hạ tại ta có tại suy ra . 
Tam giác vuông tại đường cao có .
Vậy . 
Cho khối chóp có đáy là tam giác cân tại , , ,. Gọi là góc giữa hai mặt phẳng và . Khi thì thể tích khối chóp đã cho bằng
	A..	B. .	C. .	D..
Lời giải
Chọn D
Kẻ suy ra và .
Khi đó ta có .
Chứng minh tương tự ta có suy ra tứ giác nội tiếp đường tròn đường kính . Do đó góc bằng .
Dễ thấy nên đều.
 cân tại có suy ra . 
Do đó .
Dễ thấy nên .
Trong mặt phẳng kẻ .
Trong mặt phẳng kẻ . 
Xét hai tam giác vuông và có , (vì ) 
suy ra mà và nằm giữa và nên . 
Từ đó ta có và .
Do đó .
Đặt 
Xét có .
Xét vuông tại có .
Thay vào ta có .
Vậy thể tích khối chóp là .
Cho tứ diện đều có cạnh bằng , và lần lượt là hai điểm di động trên hai cạnh ( và không trùng với ) sao cho mặt phẳng luôn vuông góc với mặt phẳng . Gọi lần lượt là thể tích lớn nhất và nhỏ nhất của tứ diện . Tính tích .
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Kẻ (vì ). Suy ra là trọng tâm của tam giác đều . 
Như vậy và là hai điểm di động nhưng luôn đi qua trọng tâm của tam giác .
Đặt , (,)
+ .
+ 	(*)
+ 	(**)
Do đó 	(***)
Mặt khác từ (*) và (**) suy ra , (,).
Đặt . Điều kiện: .
Khi đó là nghiệm của phương trình , .
Ta tìm để có nghiệm phân biệt thuộc hoặc có nghiệm kép thuộc 
Ta có không phải là nghiệm của nên .
Đặt , . Ta có: .
Bảng biến thiên của 
Dựa vào BBT, có nghiệm phân biệt thuộc hoặc có nghiệm kép thuộc 
 (thỏa điều kiện) hay . 
Kết hợp (***) ta có , .
Cho khối tứ diện đều cạnh bằng Gọi lần lượt là trọng tâm của ba tam giác Tính thể tích của khối chóp 
A. .	B. .	C. .	D. .
Lời giải
Chọn C
Tam giác đều 
.
Mà 
Lại có: .
Cho hình chóp có , , . Hình chiếu vuông góc của xuống mặt phẳng nằm bên trong tam giác . Các mặt phẳng , , đều tạo với đáy một góc . Gọi , , là các đường phân giác của tam giác với , , . Thể tích gần với số nào sau đây?
A. 	B. 	C. 	D. 
Lời giải
Chọn D
Vì các mặt phẳng , , đều tạo với đáy một góc và hình chiếu vuông góc của xuống mặt phẳng nằm bên trong tam giác nên ta có hình chiếu của chính là tâm của đường tròn nội tiếp tam giác .
Gọi là nửa chu vi tam giác thì .
Ta có : và .
Suy ra chiều cao của hình chóp là : 
Vì là phân giác của góc nên ta có : .
Tương tự : , .
Khi đó : .
Tương tự : , .
Do đó,
, với , , 
 .
Suy ra 
Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng , thể tích của khối chóp có thể tích nhỏ nhất.
A. .	B. .	C. .	D. .
Lời giải
Chọn D
Giả sử ta có: ;
Xét ta có: 
Thể tích khối chóp là: 
Xét hàm số 
; (do )
Bảng biến thiên
Vậy giá trị nhỏ nhất của thể tích là: .
Cho hình chóp có đáy là hình bình hành thỏa mãn ,. Biết tam giác cân tại , tam giác vuông tại và khoảng cách từ đến mặt phẳng bằng . Thể tích của khối chóp đã cho bằng
A. .	B. .	C. .	D. .
Lời giải
Chọn A
Nhận thấy tam giác vuông tại ( do ).
Gọi là điểm đối xứng của qua ta có tứ giác là hình chữ nhật, và tam giác là tam giác đều cạnh .
Hay 
Gọi là trung điểm của đoạn , ta có: .
Trong kẻ vuông góc với tại . Khi đó: .
Ta có ( Do ) Suy ra .
Xét tam giác có vừa là trung tuyến vừa là đường cao nên tam giác cân tại .
Xét hình chóp có đáy là tam giác đều, các cạnh bên .
Nên gọi ta có .
Tam giác vuông tại nên .
Tam giác vuông tại nên .
.
Cho hình chóp , đ