Chuyên đề Bồi dưỡng học sinh giỏi Toán Lớp 8 - Chuyên đề: Tứ giác (Có lời giải)

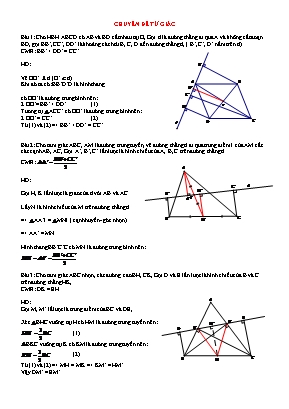
CHUYÊN ĐỀ TỨ GIÁC
Bài 1: Cho HBH ABCD có AB và BD cắt nhau tại O, Gọi d là đường thẳng đi qua A và không cắt đoạn BD, gọi BB’, CC’, DD’ là khoảng cách từ B, C, D đến đường thẳng d, ( B’, C’, D’ nằm trên d)
CMR: BB’ + DD’ = CC’
HD:
Vẽ OO’ d (O’ d)
Khi đó ta có: BB’D’D là hình thang 
có OO’ là đường trung bình nên:
2.OO’= BB’ + DD’ 	(1)
Tương tự ACC’ có OO’ là đường trung bình nên:
2.OO’ = CC’	(2)
Từ (1) và (2) => BB’ + DD’ = CC’
Bài 2: Cho tam giác ABC, AM là đường trung tuyến, vẽ đường thẳng d đi qua trung điểm I của AM cắt các cạnh AB, AC, Gọi A’, B’, C’ lần lượt là hình chiếu của A, B, C trên đường thẳng d
CMR: 
HD:
Gọi H, K lần lượt là giao của d với AB và AC
Lấy N là hình chiếu của M trên đường thẳng d
=> AA’I =MNI ( cạnh huyền- góc nhọn)
=> AA’ = MN
Hình thang BB’C’C có MN là đường trung bình nên:
Bài 3: Cho tam giác ABC nhọn, các đường cao BH, CK, Gọi D và E lần lượt là hình chiếu của B và C trên đường thẳng HK, 
CMR: DK = EH.
HD:
Gọi M, M’ lầ lượt là trung điểm của BC và DE, 
Xét BHC vuông tại H có HM là đường trung tuyến nên:
	(1)
BKC vuông tại K có KM là đường trung tuyến nên:
	(2)
Từ (1) và (2) => MH = MK => KM’ = HM’
Vậy DM’ = EM’
Bài 4: Cho tam giác ABC có G là trọng tâm, đường thẳng d không cắt các cạnh của tam giác ABC, Gọi A’, B’, C’, G’ lần lượt là hình chiếu của A, B, C, G trên đường thẳng d, 
CMR: 
HD:
Gọi M là trung điểm của AC, và D đối xứng với G qua M, 
M’ là hình chiếu của M trên d, Khi đó ta có :
=> G là trung điểm của BD 
=> GG’ là đường trung bình của hình thang BB’D’D
=> MM’ là đường trung bình của hình thang GG’D’D
Nên: 	(1)
=> DD’ + GG’ = AA’ + CC’ => DD’ = AA’ + CC’ - GG’
Thay (1) vào ta được: 2GG’ = BB’ + AA’ + CC’ - GG’
=> 3GG’ = AA’ + BB’ + CC’ => ĐPCM
Bài 5: Cho HBH ABCD và đường thẳng d nằm bên ngoài HBH, Gọi A’, B’, C’, D’ lần lượt là hình chiếu của A, B, C, D trên d,
CMR: AA’+ CC’ = BB’ + DD’
HD:
Vì ABCD là hình bình hành
nên hai đường chéo cắt nhau tại trung điểm mỗi đường
Gọi O là giao của hai đường chéo AC và BD
O’ là hình chiếu của O xuống d
Khi đó ta có: OO’ là đường trung bình của hình thang AA’C’C 
nên: 2OO’ = AA’ + CC’	(1)
Tương tự OO’ là đường trung bình của hình thang DD’B’B 
nên: 2.OO’ = DD’ + BB’	(2)
Từ (1) và (2) => AA’ + CC’ = BB’ + DD’
Bài 6: Cho tam giác ABC có trọng tâm G ( G nằm bên trong tam giác), Vẽ đường thẳng d đi qua G, cắt AB, AC, Gọi A’, B’, C’ là hình chiếu của A, B, C trên (d), Khi đó AA’, BB’, CC’ có mỗi quan hệ gì?
HD:
Gọi I trên AG sao cho AI = IG
Kẻ MM’ (d)
Khi đó ta có: 
GII’ = GMM’ (cạnh huyền = góc nhọn)
=> II’ = MM’ mà II’ = AA’ => AA’ = 2. MM’
Hình thang BB’C’C có MM’ là đường trung bình nên ta có:
 2. MM’ = BB’ + CC’
Nên ta có : AA’ = BB’ + CC’
Bài 7: Cho tam giác ABC, Gọi D là trung điểm cạnh AB, trên BC lấy các điểm E, F sao cho
 BE = EF = FC, trên tia đối của tia BA lấy điểm G sao cho BG = BD
CMR: AF, CD, GE đồng quy
HD:
Gọi I là giao điểm của CD và GE
=> E là trọng tâm của DGC => DI = IC
DEC có IF là đường trung bình nên IF // DE
Lại có: DE là đường trung bình ABF => DE // AF
Khi đó A, I, F thẳng hàng hay AF có đi qua I
Bài 8: Cho hình thang ABCD có , Gọi M là 1 điểm nằm trên đáy nhỏ AD, kẻ Mx vuông góc với BM và Mx cắt CD tại N
CMR: MB = MN
HD:
Kẻ DK //AB, chứng minh BDC vuông tại D
=> , 
Gọi H là trung điểm của BN,
Chứng minh MHBN vì BMN vuông
 mà 	(1)
Và 	(2)
Từ (1) và (2) => 
Mà: 
Vậy HMBN => BMN có MH vừa là đường cao vừa là trung tuyên nên MB = MN
Bài 9: Cho tam giác ABC có góc A tù, AC > AB, H là chân đường cao hạ từ A, về phía trong góc , dựng D và E sao cho AD vuông góc với AB, AD = AB, AE vuông góc với AC và AE = AC, M là trung điểm DE
CMR: A, H, M thẳng hàng
HD:
Dựng HBH DAEF => M là trung điểm AF => AE = DF
Mà AEAC => DFAC
ta có: 
Mà: 
ADF =ABC (c.g.c) => và 
Gọi FD cắt BC tại I, cắt AC tại N và AF cắt BC tại H’
=> , 
Hay AF BC tại H
=> A, F, H thẳng hàng => A, H, M thẳng hàng
Bài 10: Cho hình thang ABCD ( AB // CD) tia phân giác góc C đi qua trung điểm M của AD, CMR:
a, 	b, BC = AB + CD
HD:
a, Giả sử MC cắt AB tại E
Khi đó 
=> CM = EM và CD = AE
Xét BEC có: => BEC cân
Mà BM là đường trung tuyến 
=> BM là đường cao
Vậy BM EC
b, Vi BEC cân nên EB = BC => BC = EA + AB = DC + AB
Bài 11: Cho hình thang ABCD ( AB // CD), có , DB là phân giác của góc , Biết chu vi của hình thang là 20cm, Tính mỗi cạnh của hình thang
HD:
Đặt BC= a, ta có ngay:AD = AB = BC = a
Mà: 
Xét BDC có 
Mà Chu vi hình thang là 20 cm nên a + a + a + 2a = 20 => a = 4
Bài 12: Cho 3 điểm A, B, C theo thứ tự nằm trên đường thẳng d, ( AB > BC), Trên cùng 1 nửa mặt phẳng bờ là đường thẳng d, vẽ các đều, Gọi M, N, P, Q, I theo thứ tự là Trung điểm của các đoạn thẳng BD, AE, BE, CD, DE
a, CMR: 3 điểm I, M, N thẳng hàng	b, CMR: 3 điểm I, Q, P thẳng hàng	
c, CMR: MNPQ là thình thang cân	d, 
HD:
a, Dễ thấy AD // BE
IN là đường trung bình ADE => IN // AD
IM là đường trung bình DBE => IM // BE // AD
=> 3 điểm I, M, N thẳng hàng
b, Chứng minh tương tự
c, Trong AEB có NP là đường trung bình => NP // (d)
Tương tự MQ // (d) => MQ // NP
=> , 
Chứng minh tương tự ta có: 
d, Vì MNPQ thang cân => NQ = MP, Mà MP là đường trung bình BED nên:
Bài 13: Cho hình thang ABCD ( AB // CD), Gọi E là giao điểm của AD và BC, Gọi M, N, P, Q lần lượt là trung điểm của AE, BE, AC, BD, 
CMR: MNPQ là hình thang
HD:
Dễ dạng chứng minh được MN // AB
Gọi R là trung điểm của AD khi đó ta có: RQ // AB
RP // DC // AB
Nên RP // AB => R, Q, P thẳng hàng => PQ / / AB
Vậy MNPQ là hình thang
Bài 14: Cho tứ giác ABCD, Gọi P, Q theo thứu tự là trung điểm của AD và BC
a, CMR: 
b, Tứ giác ABCD là hình thang khi và chỉ khi 
HD:
a, Tự chứng minh
b, Ta chứng minh ABCD là hình thang => 
Thật vậy : ADC có pR là đường trung bình => 	(1)
RQ là đường trung bình ABC => 	(2)
Cộng theo vế (1) và (2) ta được : 
Ta chứng minh nếu thì ABCD là hình thang
Thật vậy => 3 điểm P, Q, R thẳng hàng,
Mà : PQ // DC và RQ // AB => AB // CD => ABCD là hình thang
Bài 15: Cho đều, Trên tia đối của tian AB, lấy D, trên tia đối của tia AC lấy điểm E sao cho AD=AE, Gọi M, N, P, Q theo thứ tự là các trung điểm của BE, AD, AC, AB, CMR:
a, Tứ giác BCDE là hình thang cân	b, Tứ giác CNEQ là hình thang
c, là tam giác đều
HD:
a, AED đều => 
Lại có 2 đường chéo bằng nhau => là hình thang cân
b, ABC đều => CQAD
AED đều => EN AD => CQ // En => là hình thang
c, Ta có: NP là đường trung bình => 
Xét BEP có , MP là đường trung tuyến => 
Xét ENB có và MN là đường trung tuyên => 
Vậy NMP có 3 cạnh bằng nhau nên là tam giác đều
Bài 16 : Cho tam giác ABC đều, M là điểm nằm trong tam giác, Đường thẳng qua M và // với BC cắt AB ở D, đường thẳng qua M và // với AC cắt BC tại E,đường thẳng qua M và // với AB cắt AC ở F, CMR :
a, Tứ giác : ADMF, BDMF, CFME là các hình thang cân
b, 
HD:
a, Vì ABC đều => 
và ( đồng vị) 
=> hình thang ADMF có hai góc ở đáy bằng nhau
Nên ADMF là hình thang cân
Các hình thang còn lại CMTT
b, Ta có:
MA=DF. MB=DE, MC=EF
Xét DEF => ( Bất đẳng thức trong tam giác)
Bài 17 : Cho tứ giác ABCD, có : 
CMR : ABCD là hình thang cân
HD:
Vẽ 
=> ABM =CBN ( cạnh huyền- góc nhọn)
=> BM =BN
=> BD là tia phân giác góc 
Mà ABD cân => AB// DC=> => 
Vậy ABCD là hình thang cân
Bài 18 : Cho tam giác ABC vuông tại A, Vẽ AH vuông góc với BC tại H, Gọi M, N lần lượt là trung điểm của các đoạn thẳng AH CH, CMR :
MN vuông góc với AB và BM vuông góc với AN
HD:
Vì MN là đường trung bình
=> MN//AC mà AC AB
=> MN AB=> M là trực tâm của ABN
ABN có M là trực tâm => BM AN	
Bài 19 : Cho tứ giác ABCD có AD = BC, đường thẳng đi qua trung điểm M và N của các cạnh AB và CD cắt AD và BC lần lượt ở E và F, CMR :
HD :
Gọi I là trung điểm của BD
Ta có: MI, NI lần lượt là đường trung bình
=> => IMN cân
=> ( đồng vị )
và ( so le trong)
Vậy 
Bài 20 : Cho hình thang ABCD, (AB<CD), GỌi M, N, P lần lượt là trung điểm của AB, BD, AC, đường thẳng vuông góc với MN tại N và đường thẳng vuông góc với MP tại P cắt nhau tại E, CMR: EC = ED
HD:
Gọi Q là trung điểm của CD
MN là đường trung bình => 
PQ là đường trung bình => 
Chứng minh tương tự => MNPQ là hình bìn hành
Bài 21: Cho tam giác ABC có BC = a, các đường trung tuyến BD, CE, lấy các điểm M, N trên các cạnh BC sao cho BM=MN=NC, GỌi I là giao điểm của AM và BD, K là giao điểm của AN và CE, Tính IK
HD:
Vì DN là đường trung bình của ACM => DN // AM
BDN có: => I là trung điểm của BD
Chứng minh tương tự=> K là trung điểm của EC
Kéo dài IK cắt AB và AC lần lượt tại G và H
Khi đó BED có GI đi qua trung điểm I của BD và // ED 
nên GE=GBCED có KH đi qua trung điểm K của EC và // ED 
nên HD=HC
Khi đó ta có: 
Còn 
Nên IK= GH - GI- HK=
Vậy 
Bài 22: Cho tam giác ABC nhọn, trực tâm H, M là trung điểm của BC, qua H kẻ đường thẳng vuông góc với HM, cắt AB, AC theo thứ tự tại E và F
a, Trên Tia đối tia HC, lấy điểm D sao cho HD=HC, CMR E là trực tâm của tam giác DBH
b, CMR: HE=HF
HD:
a, Ta có MH là đường trung bình BCD
 => MH// BD, 
Mà EF // MH => EF BD
Ta lại có: BADH => BDH có E là trực tâm
b, Gọi G là giao điểm của DE và BH
=> K là giao điểm BH và AC
=> DHG = CHK ( cạnh huyền - góc nhọn) => HG =HK
=> HGE = HKF ( c. g. c) => HE= HF
Bài 23: Cho hình thang ABCD, có và BC=2AB=2AD, gọi M là 1 điểm trên dây nhỏ AD, Kẻ Mx vuông góc với BM và Mx cắt CD tại N, CMR: MB =MN
HD:
Kẻ DK // AB, CMRBDC vuông tại D 
=> 
Gọi H là trung điểm của BN, 
=> MH BN vì BMN vuông
=> => MH= DH
, Mà 
và => 
Mà: 
Vậy HM BN
Bài 24: Cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE, gọi I và K theo thứ tự là hình chiếu của B và C trên đường thẳng ED, CMR: IE=DK
HD:
Gọi M là trung điểm của BC, kẻ MN ED
Tứ giác BIKC là hình thang => NI= NK 	(1)
BEC vuông có EM =. BC
 BDC vuông có DM =. BC	=> EM =DM
=> EDM cân có MN đường cao và là trung tuyến
=> NE = ND	(2)
Từ (1) và (2) => IE= DK
Bài 25: Cho hình thang ABCD (AB//CD), Gọi E và F theo thứ tự là trung điểm của BD và AC, Vẽ đường thẳng đi qua E và vuông góc với AD và đường thẳng qua F vuông góc với BC, cắt nhau tại I, CMR: IC=ID
HD:
Gọi N là trung điểm của DC
 => FN là đường trung bình của ADC
=> 
Chứng minh tương tự: 
 => I là trực tâm
=> IN EF, mà EF // DC => IN DC
IDC có IN vừa trung tuyến vừa đường cao => IDC cân => ID=IC
Bài 26: Cho đoạn thẳng AB và trung điểm O của nó, trên cùng 1 nửa mặt phẳng có bờ AB, vẽ hai tia Ax và By vuông góc với AB, Một góc vuông đỉnh O cắt Ax tại C, cắt By tại D
a, AC+BD=CD	b, CO là tia phân giác của 
HD
a, Gọi I là trung điểm của CD
AC// BD => OI là trung bình của hình thang ABCD 
=> 
=> 
Lại có COD vuông => OI là đường trung tuyến 
=> OI= CI= ID=> 2OI = IC +ID = CD
b, ta có OCD vuông tại O có OI là đường trung tuyến nên OI = IC
=> IOC cân tại I=> 
Mà: Nên => vậy OC là tia phân giác góc 
Bài 27: Cho ABC nhọn, trong đó , Lấy D là điểm bất kì trên BC, gọi E, F lần lượt là điểm đối xứng của D qua cạnh AB, AC. EF cắt AB, AC lần lượt tại M, N
a, CMR: AE=AF và Tính 	b, CMR: AD là tia phân giác DMN
HD:
a, Ta có: D và E đối xứng với nhau qua AB
nên AB là đường trung trực của ED=> AE=AD
Tương tự AD= AF
khi đó AE=AF, Ta có: 
=> 
b, Do đối xứng nên ta có: 
 và AEF cân tại A nên 
Vậy AD là phân giác góc 
Bài 28: Cho tứ giác ABCD, có các đường chéo AC và BD cắt nhau tại O, và AD vuông góc AC, BD vuông góc với CB, Gọi E là giao điểm của AD và BC, d là đường thẳng đi qua các trung điểm của EO và CD
a, CMR: A và B đối xứng nhau qua đường thẳng d
b, Tứ giác ABCD sẽ như thế nào nếu D trùng EO
HD:
a, Ta có: Gọi I, K lần lượt là trung điểm của OE và BC
Ta có:
AOE vuông tại A có Ai là trung tuyến 
nên AI= IE=IO	(1)
BOE vuông tại B có BI là đường trung tuyến 
nên BI=EI=IO	(2)
Từ (1) và (2) ta có: IA = IB
Tương tự ADC vuông tại A có AK là đường trung tuyến 
=> AK = DK=CK
BDC có BK là đường trung tuyến của tam giác vuông nên BK = KD= KC
Nên KA= KB hay K nằm trên đường trung trực AB
Vậy IK là trung trực của AB hay A và B đối cứng với nhau qua (d)
b, Ta thấy EO là đường thẳng chứa đường cao của EDC
Nếu d trùng với Eo thì d vừa là đường trung trực AB và CD nên ABCD là hình thang cân
Bài 29: Cho HBH ABCD, Gọi E, F lần lượt là trung điểm của AD, BC, đường chéo AC cắt BE, DF lần lượt tại P và Q, gọi R là trung điểm của đoạn thẳng BP, CMR:
a, AP=PQ=QC	b, Tứ giác ARQE là hình bình hành
HD:
a, Trong BDC có CO và DF là hai đường trung tuyến 
nên Q là trọng tâm
=> 
Tương tự ABD có P là trọng tâm
=> 
Từ (1) và (2) ta có AP= QC
Ta lại có :
vậy AP= PQ= QC
b, Vì P là trọng tâm ABD nên 
Tứ giác ARQE có hai đường chéo cắt nhau tịa trung điểm mỗi đường nên là HBH
Bài 30: Cho tam giác ABC, ba điểm N, P, Q theo thứ tự là trung điểm của AB, BC, AC, và I, J, K lần lượt là TĐ của các đoạn thẳng NP, BP, NC.
CMR: IJKQ là hình bình hành
HD:
Ta có:
 NPB có IP =IN ( gt) và JP =JN (gt)
Nên Ị là đường trung bình => IJ // NB và IJ =NB
Tương tự ta có: QK // AN và QK =. AN=NB
Từ đó ta có: IJKQ là hình bình hành
Bài 31: Cho tam giác ABC (AB<AC), Dựng vè phía ngoài các ABD cân tại B, ACE cân tại C sao cho , Gọi M là trung điểm BC, so sánh MD và ME
HD:
Dựng HBH ABFC
Ta chứng minh được BDF= CFE => FD= FE
Ta chứng minh AD<AE
Từ đó 
Bài 32: Cho ABC có , các đường phân giác BD và CE cắt nhau tại I, qua E kẻ đường thẳng vuông góc với BD cắt BC ở F, CMR:
a, E và F đối xứng nhau qua BD	b, IF là phân giác 
c, D và F đối xứng nhau qua IC
HD:
a, EBF cân tại B, BD là tia phân giác góc , 
nên BD là đường trung trực EF, vậy E, F đối xứng với nhau qua BD
b, Tính nên 
vậy IF là tia phân giác 
c, IDC =IFC (g.c.g) => IF =ID, CF= CD
Do đó: CI là đường trung trực của DF
Vậy D, F đối xứng với nhau qua CI
Bài 33: Cho hình thang vuông ABCD , có CD= 2AB, gọi H là hình chiếu của D trên AC, M là trung điểm của HC, CMR: 
HD:
Gọi N là trung điểm của HD, ta có: MN là đường trung bình
=> 
Mà: 
nên AB// MN và AB= MN => ABMN là hình bình hành
=> AN//BM
 ADM có DH AM, MN AD, AN DM
Khi đó 
Bài 34: Cho ABC cân tại A, lấy điểm D trên AB, E trên AC sao cho AD=CE, gọi I là trung điểm của DE, K là giao điểm AI và BC
CMR: ADKF là HBH
HD:
Kẻ DM, IN // BC, Hãy chứng minh AM = CE
Vì MN =NE=> N là trung điểm AC
=> I là trung điểm AK
Tứ giác ADKE có hai đường chéo cắt nhau 
tại trung điểm mỗi đường nên là HBH
Bài 35: Cho tam giác ABC đều, một đường thẳng // với BC cắt AB, AC ở D và E, Gọi D là trọng tâm của tam giác ADE, I là trung điểm của CD, Tính số đo các góc của tam giác GIB
HD:
Qua C vẽ đường thẳng song song với BD, cắt DE tại K
Ta có: BDKC là hình bình hành=> B, I, K thẳng hàng
Chứng minh GDB= GEK (c.g.c)
Để GBK cân tại G có , 
do đó các góc của GBI lần lượt là 
Bài 36: Cho ABC, kẻ đường cao AH, Gọi D và E theo thứ tự là các điểm đối xứng với H qua AB và AC, đường thẳng DE cắt AB, AC lần lượt tại M, N
a, CMR:DAE cân	b, CMR: HA là phân giác 
c, CME : 3 đường thẳng BN, CM, AH thẳng hàng
d, CMR : BN, CM là các đường cao của ABC
HD:
a, Ta có: AD= AH, AE = AH => AD = AE
b, Do Tính chất đối xứng ta => AB là phân giác 
Kẻ 	(1)
AC là phân giác , Kẻ AK HN=> AK= AJ	(2)
Từ (1) và (2) ta có: AI = AK
Vậy A cách đều 2 cạnh góc 
=> HA là phân giác góc 
c, Chứng minh tương tự ta cũng có: CM là tia phân giác 
BN là tia phân giác góc 
Trong MHN các đường phân giác trong HA, MC, NB cùng đồng quy tại 1 điểm
d, AB là phân giác góc 
 MC là phân giác góc , mà 2 góc kề bù => MCAB 
=> MC là đường cao ABC
Chứng minh tương tự BN là đường cao của ABC
Bài 37: Cho hình thang vuông ABCD, (AB//CD), gọi E , F theo thứ tự là các điểm đối xứng của B và điểm A qua đường thẳng DC, G, H theo thứ tự là các điểm đối xứng của C và E qua AD
a, CMR: D là trung điểm của BH	b, CMR: AH// BF, CH// BG
HD:
a, Gọi I là giao BE và DC, do tính chất đối xứng ta có:
BI =IE, Mà DF =AD và AD=BI=> DF =BI
Ta cũng có: DI= HF
Hai tam giác vuông BID và DFH bằng nhau 
cho ta DB= DH 	(1)
Và 
=> H, B, D thẳng hàng	(2)
Từ (1) và (2) => D là trung điểm BH
b, Dễ dạng chứng minh được ADH = FDB => 
Dễ chứng minh được BDG = HDC => 
Bài 38: Cho ABC, Gọi D, E, F theo thứ tự là trung điểm của các cạnh AB, AC, BC và I, J, K theo thứ tự là trung điểm của DF, BF, CD
a, CMR: Tứ giác IJFK và IEKJ là hình bình hành
b, 3 điểm E, K, F thẳng hàng
HD:
a, Ta có: IJFK là hình bình hành
Chứng minh tương tự cho tứ giác IEKJ
b, DE// FC và DE =FC
=> DECF là hình bình hành 
=> EF đi qua trung điểm K của DC
Vậy E, K, F thẳng hàng
Bài 39: Cho HBH ABCD có , Tia phân giác góc D đi qua trung điểm I của AB, Kẻ AH vuông góc với DC, CMR:
a, AB=2AD	b, DI=2AH	c, AC vuông góc AD
HD:
a, DAI cân đỉnh A
=> AD = AI= 
b, Kẻ AH DC, AM DI
=> ADM = ADH => AH= DM = DI
c, ADC có vuông tại A
Bài 40: Cho HBH ABCD, lấy hai điểm E, F trên BD sao cho 
a, CMR: AECF là HBH
b, Gọi K là giao điểm của CE và AB, I là trung điểm của AK, Xác định vị trí E sao cho AI=IK=KB
HD:
a, Xét ABE và CDF ta có:
AB= CD, và BE= CF => ABE=CDF (c. g.c)
=> AE= CF
Chứng minh tương tự AF = CE=> AECF là hình bình hành
b, Ta có:	
 Khi đó: => E là trung điểm OB
Bài 41: Cho ABC, kẻ các đường cao BD và CJ, Gọi H là trực tâm của , E là trung điểm của AH, D là trung điểm của BC, CMR: I và J đối xứng với nhau qua ED
HD:
BIC vuông tại I có ID là trung tuyến ứng với cạnh huyền BC
=> 
Chứng minh tương tự: 
Chứng minh tương tự: JE= EI
=> ED là đường trung trực của IJ
=> IJ đối xứng nhau qua ED 
Bài 42: Cho ABC, Về phía ngoài tam giác vẽ các ABD vuông cân tại B, ACE vuông cân tại C, Gọi M là trung điểm của DE, CMR: MBC vuông cân
HD:
Trên nửa mặt phẳng bờ BC, Vẽ BCN vuông cân tại C
=> ABC = ENC (c.g.c)
=> 
=> (K là giao điểm cảu EN và AB)
Ta lại có : BD=NE (= AB) 
=> BD// NE ( Cùng vuông góc với AB)
=> BDNE là hình bình hành
=> M là trung điểm BN
Mà CBN vuông cân tại C => MBC vuông cân tại M
Bài 43: Cho ABC có ba góc nhọn (AB<AC), gọi H là trực tâm, O là giao điểm của 3 đường trung trực của tam giác, D là điểm đối xứng của A qua O
a, CMR: Tứ giác BHCD là HBH
b, Gọi M là trung điểm của BC, CMR : AH=2.MO
HD: 
a, Từ AO= OC = OD
=> Chứng minh ,
ta có: DCAC, BHAC ( H là trực tâm của ABC)
=> BH // DC
Chứng minh tương tự ta cũng có: CH// DB
Vậy BHCD là Hình bình hành
b, M là trung điểm của BC
=> M là trung điểm của HD
Mà O là trung điểm của AD => OM là đường trung bình của AHD
=> OM = AH => AH= 2OM
Bài 44: Cho ABC cân tại A, từ 1 điểm D bất kỳ trên đáy BC, vẽ đường thẳng vuông góc với BC cắt các đường thẳng AB, AC ở E và F, Vẽ các HCN BDEH, CDFK
CMR:A là trung điểm của HK
HD:
Gọi I và O là tâm của HCN BDEH và CDFK, Ta có:
 Mà 
=> BE// DK, DH// CA
=> AIDO là hình bình hành nên AO = ID
mà HI = ID, Nên AO = HI
Ta lại có: AO // HI nên AOIH là hình bình hành
Do đó:
AH // IO, AH= IO 	(1)
Chứng minh tương tự ta có:
AIOK là hình bình hành => AK// IO và AK=IO 	(2)
Từ (1) và (2) ta có: H, A, K thẳng hàng và AH= AK
Bài 45: Cho HBH ABCD, Các đường cao AE và AF, biết AC =25cm, EF=24cm, Tính khoẳng cachs từ A đến trực tâm H của AEF
HD:
Kẻ CN vuông góc với AB, 
Tứ giác EHFC có EH // CF, HF// FC
nên EHFC là hình binh hành => AN = HF ( = EC)
Tứ giác ANFH có AN = HF, AN// HF
nên là hình bình hành => AH + NF, AH// NF
Lại có AH EF nên NF EF
EFN vuông tại F có EF =24cm, NE = AC= 25cm nên
Bài 46: Cho ABC, Trực tâm H, I là giao điểm các đường trung trực, Gọi E là điểm đối xứng với A qua I, CMR: BHCE là hình bình hành
HD:
Gọi I là giao của 3 đường trung trực => IA = IB = IC
Lại có: IA = IE nên IA= IB= IE= IC
Chứng minh AC CE để suy ra BH// EC
tương tự CH// BE
Bài 47: Cho H là hình chiếu của B trên đường chéo AC của HCN ABCD, M và K theo thứ tự là trung điểm của AH và CD
a, Gọi I và O theo thứ tự là trung điểm của AB và IC, CMR: 
b, Tính số đo ?
HD:
Ta có: BIKC là Hình chữ nhật nên O là trung điểm của IC và BK
Xét IMC vuông, Ta có : MO= DC
b, MBK có MD = IC=BK, Nên 
Bài 48: Cho ABC vuông cân tại A có AH là đường cao, Gọi M là 1 điểm bất kỳ trên cạnh BC, I và K là hình chiếu vuông góc của M trên AB, AC, CMR: IHK vuông cân
HD:
Chứng minh AIMK là hình chữ nhật
Vì ABC vuông cân tại A
=> AK= IM = BI
mà BH = HA => 
=> BHI = AHK (c. g. c)
=> IH = HK
Mà 
Bài 49: Cho HCN ABCD, Kẻ BH vuông góc với AC, Gọi M và K lầ lượt là trung điểm của HC và AD, CMR: BK vuông góc với KM
HD:
AKB, kẻ đường cao KI cắt BH tại E
=> E là trực tâm của AKB=> AE BK
Ta có : KI// AD và KI //BC => KE // MA và KE =MA
=> Tứ giác AMKE là hình bình hành
 => AE//MK mà AE BK=> MK BK
Bài 50: Cho ABC nhọn, Trực tâm H, giao điểm của các đường trung trực là O, Gọi P, Q, N theo thứ tự là trung điểm của các đoạn thẳng AB, AH, AC
a, CMR: OPQN là HBH
b, ABC cần có điều kiện gì để OPQN là HCN
HD:
a, Gọi O là giao của 3 đường trung trực nên 
Trong AHC, QN là đường trung bình nên QN// HC
Và PO //HC ( cùng vuông góc với AB)
Chứng minh tương tự ta có: OPQN là hình bình hành
b, ta có: tứ giác BCQN là hình chữ nhật có 2 đường chéo là NC và BQ 
=> NC = BQ
=> , 
Xét MQB có MP là đường trung tuyến nên MP = BQ
nên MBQ vuông tại M => MB MQ
Bài 51: Cho ABC cân tại A, từ 1 điểm D bất kỳ trên đáy BC, vẽ đường thẳng vuông góc với BC cắt các đường thẳng AB, AC ở E và F, Vẽ các HCN BDEH, CDFK, Gọi I, J lần lượt là tâm các HCN BDEH và CDFK, M là trung điểm của AD
a, CMR: Trung điểm HK là 1 điểm có định không phụ thuộc vào vị trí của D trên BC
b, CMR: 3 điểm I, J, M thẳng hàng và 3 đường thẳng AD, HJ, KI đồng quy
HD:
a, Ta có: mà 
Chứng minh tương tự ta có: JD// AB
Khi đó AIDJ là hình bình hành=> AJ // ID, AJ = ID
=> Chứng minh AHIJ là hình bình hành
=> IJ // AH và IJ = AH và IJ //AK và IJ =AK
Khi đó 3 điểm A, H, K thẳng hàng và A là trung điểm của HK
b, Tứ giác AIDJ là hình bình hành
=> M là trung điểm của AD, 
thì M nằm trên đường chéo của HBH
Bài 52: Cho HCN ABCD và 1 điểm M thuộc miền trong của HCN
a, Gọi E, F, G, H là các điểm đối xứng của M theo thứ tự qua các trục AB, BC, CD, DA, CMR: E, F đối xứng với nhau qua điểm B. E và H đối xứng với nhau qua A. G và H đối xứng với nhau qua D. F và G đối xứng với nhau qua C
b, Chọn M sao cho EFGH là HBH, khi đó EFGH là hình gì?
HD:
a, Do tính chất của đối xứng trục nên 
=> 	
=> 3 điểm E, B, F thẳng hàng
Mà BE = BM = BF
=> E, F đối xứng với nhau qua B
Các điểm khác chứng minh tương tự
b, Để EFGH là hình bình hành thì EF// HG//AO, Khi đó M trùng với O, Tâm của HCN 
=> EFGH là hình thoi
Bài 53: Cho ABC có trực tâm H, Gọi M là trung điểm của BC, Gọi D là điểm đối xứng với H qua M, Gọi I là trung điểm của AD, CMR: IM vuông góc BC
HD:
Vì IM là đường trung bình của AHD
 => 
Bài 54: Cho ABC, kẻ đường cao AH, gọi I là trung điểm của AC, E là điểm đối xứng với H qua I, Gọi M và N lần lượt là trung điểm của HC và CE, các đường thẳng AM, AN cắt HE tại G và K
a, CMR: Tứ giác AHCE là HCN	b, CMR : HG=GK=KE
HD;
a, Tự chứng minh
b, G là trọng tâm AHC => HG = 2 GI
Chứng minh tương tự ta có: KE= 2. KI
mà IH = IE=> IG= IK => GK =2.GI=2.IK=> ĐPCM
Bài 55: Cho HBH ABCD có AB=2AD, Góc vẽ BH vuông góc với AD, . Gọi M, N theo thứ tự là trung điểm của CD và AB
a, CMR: ANMD là hình thoi
b, Tính 
HD:
a, Tự chứng minh
b, Ta có:
, Tính 
Ta có: ( So le trong)
Mà : 
Xét HAN cân tại N => 
=> , Vậy 
Bài 56: Cho ABC vuông tại A, đường cao AH, trung tuyến AM, Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC	,CMR:
a, AH= DE	b, 	c, 
d, DI//EK, với I là trung điểm của HB, K là trung điểm của HC
HD:
a, Tứ giác ADHE có 3 góc vuông nên là HCN => AH= DE
b, ABC vuông tại A, Có AM là đường trung tuyến => AM= MB= MC
=> AMC cân tại M => 
Mặt khác , 
Vì cùng phụ với 
c, Chứng minh AM, Ta có: , ta có:
d, Ta có: HEC có EK = KH = KC => EKC cân tại K 
=> 
=> EK //AM => KE DE, Chứng minh tương tự
=> 
Bài 57: Cho ABC, Trên tia đối của tia BA lấy D, trên tia đối của tia CA lấy E sao cho BD=CE=BC, Gọi M là giao điểm của BE và CD, đường thẳng song song với tia phân giác của góc cắt AC ở F, 
CMR:AB=CF
HD:
Vẽ Hình bình hành ABNC => AB = NC
=> CB= CE=> BCE cân
=> 
=> BM là tia phân giác góc , CM là tia phân giác 
=> NM // phân giác góc 
=> 3 điểm F, M, N thằng hàng
=> 
=> NFC cân tại C
=> NC = CF mà NC = AB => AB= CF
Bài 58: Cho HCN ABCD, M là điểm bất kỳ nằm trong HCN, vẽ ME AB tại E, MF AD tại F, CK AM tại K, CMR:
a, 	b, 	 c, 
HD
a, Tứ giác AEMF là hình chữ nhật 
=> MA= EF => 
b, Gọi G là giao điểm của EM và CD, 
H là giao điểm của FM và BC
=> Tứ giác DFMG, GMHC, EBHM là hình chữ nhật,
Do vậy 
=> ĐPCM
c, Gọi O là giao của 2 đường chéo AC và BD 
=> 
Bài 59: Cho ABC vuông tại A (AC>AB), đường cao AH, trên HC lấy HD=HA, đường BC tại D cắt AC tại E
a, CMR: AE =AB	b, M là TĐ của BE, Tính 
HD:
a, Chứng minh AE=AB
Kẻ EF AH => tứ giác HDEF là hình chữ nhật 
=> HBA=FAE (g.c.g) => AB=AE
b, ABE vuông cân tại A=> 
BDE vuông cân tại D=> 
Từ đó ta có: AM=MD
Xét AHM = DHM (c. c. c)=> 
Bài 60: Cho ABC, D trên AB, E trên AC sao cho BD=CE, Gọi M, N là trung điểm của BC, DE, Vẽ các hình bình hành BDNI và CENK
a, CMR: I, M, K thẳng hàng
b, MN cắt AC tại Q, cắt BA tại P, CMR: APQ cân
HD:
a, Tứ giác BDNI là hình bình hành => 
Tứ giác NECK là hình bình hành => 
Từ đó ta có KC//DE và BI= KC
=> Tứ giác BICK là hình bình hành có M là trung điểm của BC
=> M đi qua trung điểm IK => I, K, M thẳng hàng
b, Ta có: NI=DB, NK= CE mà BD = CE => NI = NK => NIK cân tại N
Mà MN là đường trung tuyến => NM là phân giác => 
Lại có : NK // QC=> ( đồng vị)
và NI// BD=> ( đồng vị )
=> ( đối đỉnh) => 
Vậy APQ cân tại A
Bài 61: Cho HCN ABCD, qua E trên đường chéo AC, kẻ đường // với BD cắt AD và phần kéo dài của CD ở M và N, Vẽ HCN DMFN, CMR:
a, FD//AC	b, E là trung điểm của FB
HD:
a, Chứng minh FD// AC
Tứ giác ABCD là hình chữ nhật, 
AC cắt BD tại O => OC= OD => , 
Mà EN // BD => Mà IND cân
=> => FD//AC
b, Chứng minh DIEO là hình bình hành => DI//EO và DI =EO => FI//EO và FI =EO
=> FIOE là hình bình hành
=> IO //EF và IO =EF	(1)
Mặt khác IO là đường trung bình của DFB => OI =EB	(2)
Từ (1) và (2) => EB= EF
Bài 62: Cho ABC nhọn, vẽ các đường cao AD và BE, Tia phân giác Ax của cắt BE và BC lần lượt ở M và N, Tia phân giác By của cắt AD và AC lần lượt tại P và Q, CMR:
a, ANBQ	b, Tứ giác MPNQ là hình thoi
HD:
a, Ta có: ( cùng phụ góc C)
=> 
EBQ vuông => 
=> 
b, APQ có AO vừa là đường phân giác vừa là đường cao
 => AO là đường trung trực
=> MP= MQ, NP= NQ
BMN có BO vừa là đường phân giác vừa là đường cao=> là đường trung trực => ĐPCM
Bài 63: Cho hình vuông ABCD, Từ điểm M tùy ý trên đường chéo BD, kẻ ME, MF lần lượt vuông góc với AB và AD, CMR:
a, CF=DE, CFDE	b, CM=EF, OMEF
c, CM, BF, DE đồng quy	d, Xác định M để diện tích AEMF lớn nhất
HD:
a, BD là đường chéo của hình vuông ABCD 
=> BD là phân giác góc D
=> cân tại F=> DF=FM=AE
CDF= DAE (c.g.c) => CF = DE và 
Mà 
b, AM =EF, BD là đường trung trực của AC 
=> MA =MC=> MC= EF
Kéo dài FM cắt BC tại N => Tứ giác BEMN là hình vuông, => MN= ME
=>EMF= MNC(c. g. c) => , Mà 
=> => ĐPCM
c, EFC có CHEF=> CM trùng CH là đường cao ứng với cạnh EF
Lại có EDCF tại O=> ED là đường cao ứng với cạnh CF
Chứng minh tương tự câu a=> CEBF=> BF là đường cao ứng với cạnh CE
=> 3 đường CM, BF, DE đồng quy
Bài 64: Cho tam giác ABC, trên tia đối của tia BC, lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=BC=CE, Qua D kẻ đường thẳng // với AB cắt AC ở H, qua E kẻ đường thẳng // với AC cắt AB ở k, chúng cắt nhau ở I
a, Tứ giác BHKC là hình gì?	b, Tia IA cắt BC tại M, CMR : MB=MC
c, Tìm điều kiện của ABC để tứ giác DHKE là hình thang cân
HD:
a, Tứ giác BHKC là hình bình hành vì 
có 2 đường chéo BK và HC cắt nhau tại trung điểm của mỗi đường
b, Tứ giác AHIK cũng là hình bình hành, nên AK// IH và AK= IH
AB//IH và AB=IH
=> ABHI là hình bình hành
=> IA// HB=> AM là đường trung bình của HBC 
=> BM = MC
c, Tứ giác DHKE là hình thang vì HK //DE, 
để là hình thang cân => 
Hay cân tại A
Bài 65: Cho hình thang vuông ABCD, , CD=2AB=2AD, Gọi H là hình chiếu của D lên AC. Gọi M, P, Q lần lượt là trung điểm của CD, HC và HD
a, CMR: Tứ giác ABMD là hình vuông và tam giác BDC là tam giác vuông cân
b, CMR: DMPQ là hình bình hành
c, CMR: AQ vuông góc với DP
HD:
a, Chứng minh tứ giác ABMD có 4 cạnh bằng nhau, 
lại có nên ABMD là hình vuông
BCD có MB= MC=MD nên là tam giác vuông , 
lại có 
Do đó: BDC là tam giác vuông cân ở B
b, Tứ giác DMPQ là hình bình hành vì có PQ// DM và PQ = DM
c, Chứng minh Q là trực tâm của ADP
Bài 66: Cho tam giác ABC, về phía ngoài của tam giác vẽ hai hình vuong ABEF và ACGH, CMR: các đường BG và CE cắt nhau tại 1 điểm nằm trên đường cao AD của tam giác ABC
HD:
Trên tia đối của tia AD lấy điểm K sao cho AK= B
=> ( cùng phụ )
=> EBC = BAK (c.g.c)
=> , Mà 
=> hay BKEC
Chứng minh tương tự => CK BG=> AD, BG, 
CE là ba đường cao BCK
Bài 67: Cho hình vuông ABCD, các điểm E, F lần lượt trên các cạnh BC, CD sao cho , Trên tia đối của tia DC lấy điểm M sao cho DM =BE, CMR:
a, 
b, Chu vu tam giác CEF bằng 1 nửa chu vi tứ giác ABCD
HD:
a, ABE = ADN ( 2 cạnh góc vuông)
=> 
=> 
b, AEF = AMF (c.g.c)
=> EF = MF, EF = MD+DF=BE+DF
	Chu vi CEF = CE+EF+CF
= CK+BE+DF+CF= BC+CD= chu vi ABCD
Bài 68: Cho ABC đều, đường cao AD, M là điểm nằm giữa B và D, gọi N là Trung điểm của AM, vẽ ME vuông góc AB tại E, M