Các bài toán hình học thường gặp trong kỳ thi học sinh giỏi toán 8

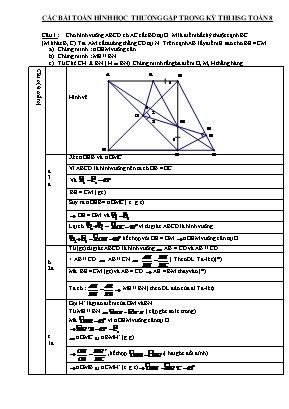
CÁC BÀI TOÁN HèNH HỌC THƯỜNG GẶP TRONG KỲ THI HSG TOÁN 8
Cõu 1 : Cho hỡnh vuụng ABCD cú AC cắt BD tại O. M là điểm bất kỳ thuộc cạnh BC 
(M khỏc B, C).Tia AM cắt đường thẳng CD tại N . Trờn cạnh AB lấy điểm E sao cho BE = CM.
Chứng minh : ∆OEM vuụng cõn. 
Chứng minh : ME // BN.
Từ C kẻ CH BN ( H BN). Chứng minh rằng ba điểm O, M, H thẳng hàng.
Cõu 4( 6 điểm)
Hỡnh vẽ
a
3
đ
Xột ∆OEB và ∆OMC
Vỡ ABCD là hỡnh vuụng nờn ta cú OB = OC 
 Và 
 BE = CM ( gt )
Suy ra ∆OEB = ∆OMC ( c .g.c)	
 OE = OM và 
Lại cú vỡ tứ giỏc ABCD là hỡnh vuụng
 kết hợp với OE = OM ∆OEM vuụng cõn tại O
b
2đ
Từ (gt) tứ giỏc ABCD là hỡnh vuụng AB = CD và AB // CD
+ AB // CD AB // CN ( Theo ĐL Ta- lột) (*)
Mà BE = CM (gt) và AB = CD AE = BM thay vào (*)
Ta cú : ME // BN ( theo ĐL đảo của đl Ta-lột)
c
1đ
Gọi H’ là giao điểm của OM và BN
Từ ME // BN ( cặp gúc so le trong)
Mà vỡ ∆OEM vuụng cõn tại O
∆OMC ∆BMH’ (g.g)
 ,kết hợp ( hai gúc đối đỉnh)
∆OMB ∆CMH’ (c.g.c) 
Vậy 
Mà CH BN ( H BN) H H’ hay 3 điểm O, M, H thẳng hàng ( đpcm)
Cõu 2: Cho hỡnh bỡnh hành ABCD cú đường chộo AC lớn hơn đường chộo BD. Gọi E, F lần lượt là hỡnh chiếu của B và D xuống đường thẳng AC. Gọi H và K lần lượt là hỡnh chiếu của C xuống đường thẳng AB và AD.
Tứ giỏc BEDF là hỡnh gỡ ? Hóy chứng minh điều đú ? 
Chứng minh rằng : CH.CD = CB.CK
Chứng minh rằng : AB.AH + AD.AK = AC2.
A
Ta cú : BEAC (gt); DFAC (gt) => BE // DF
Chứng minh : 
=> BE = DF
Suy ra : Tứ giỏc : BEDF là hỡnh bỡnh hành.
B
Ta cú: 
Chứng minh : 
B,
Chứng minh : 
Chứng minh : 
Mà : CD = AB 
Suy ra : AB.AH + AB.AH = CF.AC + AF.AC = (CF + AF)AC = AC2 (đfcm).
Cõu 3. Cho hỡnh vuụng ABCD, M là một điểm tuỳ ý trờn đường chộo BD. Kẻ MEAB, MFAD.
a. Chứng minh: 
b. Chứng minh ba đường thẳng: DE, BF, CM đồng quy.
c. Xỏc định vị trớ của điểm M để diện tớch tứ giỏc AEMF lớn nhất.
Cõu 3
(6 điểm)
HV + GT + KL 
a. Chứng minh: 	
 đpcm
b. DE, BF, CM là ba đường cao của đpcm
c. Cú Chu vi hỡnh chữ nhật AEMF = 2a khụng đổi
 khụng đổi
 lớn nhất (AEMF là hỡnh vuụng)
 là trung điểm của BD.
Bài 4: Hỡnh thang ABCD (AB // CD) cú hai đường chộo cắt nhau tại O. Đường thẳng qua O và song song với đỏy AB cắt cỏc cạnh bờn AD, BC theo thứ tự ở M và N.
a, Chứng minh rằng OM = ON.
b, Chứng minh rằng .
c, Biết SAOB= 20082 (đơn vị diện tớch); SCOD= 20092 (đơn vị diện tớch). Tớnh SABCD. 
Bài 6 (5 điểm)
a, (1,5 điểm)
Lập luận để cú , 
0,5đ
Lập luận để cú 
0,5đ
 OM = ON
0,5đ
b, (1,5 điểm)
Xột để cú (1), xột để cú (2)
Từ (1) và (2) OM.()
0,5đ
Chứng minh tương tự ON. 
0,5đ
từ đú cú (OM + ON). 
0,5đ
b, (2 điểm)
, 
0,5đ
Chứng minh được 
0,5đ
Thay số để cú 20082.20092 = (SAOD)2 SAOD = 2008.2009
0,5đ
Do đú SABCD= 20082 + 2.2008.2009 + 20092 = (2008 + 2009)2 = 40172 (đơn vị DT)
0,5đ
Bài 5:Cho tam giác ABC vuông tại A (AC > AB), đờng cao AH (HBC). Trên tia HC lấy điểm D sao cho HD = HA. Đờng vuông góc với BC tại D cắt AC tại E.
Chứng minh rằng hai tam giác BEC và ADC đồng dạng. Tính độ dài đoạn BE theo .
Gọi M là trung điểm của đoạn BE. Chứng minh rằng hai tam giác BHM và BEC đồng dạng. Tính số đo của góc AHM
Tia AM cắt BC tại G. Chứng minh: .
4.1
+ Hai tam giác ADC và BEC có: 
 Góc C chung. 
 (Hai tam giác vuông CDE và CAB đồng dạng)
 Do đó, chúng dồng dạng (c.g.c). 
Suy ra: (vì tam giác AHD vuông cân tại H theo giả thiết).
Nên do đó tam giác ABE vuông cân tại A. Suy ra: 
4.2
Ta có: (do )
mà (tam giác AHD vuông vân tại H)
nên (do )
Do đó (c.g.c), suy ra: 
4.3
Tam giác ABE vuông cân tại A, nên tia AM còn là phân giác góc BAC.
Suy ra: , mà 
Do đó: 
 Bài 6: Cho tam giác ABC vuông tại A (AC > AB), đờng cao AH (HBC). Trên tia HC lấy điểm D sao cho HD = HA. Đờng vuông góc với BC tại D cắt AC tại E.
Chứng minh rằng hai tam giác BEC và ADC đồng dạng. Tính độ dài đoạn BE theo .
Gọi M là trung điểm của đoạn BE. Chứng minh rằng hai tam giác BHM và BEC đồng dạng. Tính số đo của góc AHM
Tia AM cắt BC tại G. Chứng minh: .
4.1
+ Hai tam giác ADC và BEC có: 
 Góc C chung. 
 (Hai tam giác vuông CDE và CAB đồng dạng)
 Do đó, chúng dồng dạng (c.g.c). 
Suy ra: (vì tam giác AHD vuông cân tại H theo giả thiết).
Nên do đó tam giác ABE vuông cân tại A. Suy ra: 
Ta có: (do )
mà (tam giác AHD vuông vân tại H)
4.2
nên (do )
Do đó (c.g.c), suy ra: 
4.3
Tam giác ABE vuông cân tại A, nên tia AM còn là phân giác góc BAC.
Suy ra: , mà 
Do đó: 
Cõu 7: Cho hỡnh thang ABCD (AB // CD, AB < CD). Qua A vẽ đường thẳng song song với BC cắt BD ở E và cắt CD ở K. Qua B kẻ đường thẳng song song với AD cắt AC ở F và cắt CD ở I. Chứng minh rằng:
 a) DK = CI
 b) EF // CD
 c) AB2 = CD.EF
a) 
 Tứ giỏc ABCK cú: 
 AB // CK (AB // CD, K CD)
 AK // BC (gt)
 ABCK là hỡnh bỡnh hành
 CK = AB
 DK = CD – CK = CD – AB (1)
 Chứng minh tương tự, ta cú DI = AB
 IC = CD – DI = CD – AB (2)
 Từ (1) và (2) suy ra: DK = IC
b) 
 DEK cú AB // DK, theo hệ quả định lý Ta-let ta cú:
 (3)
FIC cú AB // IC, theo hệ quả định lý Ta-let ta cú:
 (4)
 Mà: DK = IC (cõu a) (5)
 Từ (3), (4), (5) suy ra: 
 AKC cú EF // KC (định lý Ta-lột đảo)
 EF // CD
5
c) 
 Ta cú: (vỡ AB = CK) (6)
 BCD cú EK // BC, theo định lý Ta-lột ta cú:
 (7)
 BDI cú EF // DI, theo định lý Ta-let ta cú:
 Mà DI = AB
 Suy ra: (8)
 Từ (6), (7), (8) suy ra: 
 AB2 = CD. EE
Cõu 8: Cho hỡnh vuụng ABCD, trờn cạnh AB lấy điểm E và trờn cạnh AD lấy điểm F sao cho AE = AF. Vẽ AH vuụng gúc với BF (H thuộc BF), AH cắt DC và BC lần lượt tại hai điểm M, N.
1. Chứng minh rằng tứ giỏc AEMD là hỡnh chữ nhật.
2. Biết diện tớch tam giỏc BCH gấp bốn lần diện tớch tam giỏc AEH. Chứng minh rằng: AC = 2EF.
3. Chứng minh rằng: .
Cõu 4
1
(2.0 điểm)
Ta cú (cựng phụ )
 AB = AD ( gt) 
 (ABCD là hỡnh vuụng) 
 (g.c.g) 
 => DM=AF, mà AF = AE (gt) 
 Nờn. AE = DM 
 Lại cú AE // DM ( vỡ AB // DC )
Suy ra tứ giỏc AEMD là hỡnh bỡnh hành
Mặt khỏc. (gt) 
Vậy tứ giỏc AEMD là hỡnh chữ nhật
2
(2.0 điểm)
Ta cú (g.g) 
 hay ( AB=BC, AE=AF) 
Lại cú (cựng phụ )
 (c.g.c)
, mà (gt) nờn BC2 = (2AE)2
 BC = 2AE E là trung điểm của AB, F là trung điểm của AD 
Do đú: BD = 2EF hay AC = 2EF (đpcm)
3
(2.0 điểm)
Do AD // CN (gt). Áp dụng hệ quả định lý ta lột, ta cú: 
Lại cú: MC // AB ( gt). Áp dụng hệ quả định lý ta lột, ta cú:
 hay 
 (Pytago) 
 (đpcm)
Cõu 9: Cho tam giỏc ABC vuụng tại A. Lấy một điểm M bất kỳ trờn cạnh AC. Từ C vẽ một đường thẳng vuụng gúc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E.
 	a) Chứng minh: EA.EB = ED.EC.
 	b) Chứng minh rằng khi điểm M di chuyển trờn cạnh AC thỡ tổng BM.BD+CM.CA cú giỏ trị khụng đổi.
 	c) Kẻ. Gọi P, Q lần lượt là trung điểm của cỏc đoạn thẳng BH, DH. Chứng minh .
4
 a) Chứng minh EA.EB = ED.EC. Chứng minh EBD đồng dạng với ECA (g-g)	
- Từ đú suy ra 	
 b) Kẻ MI vuụng gúc với BC (. Ta cú BIM đồng dạng với BDC (g-g)
 (1)
Tương tự: ACB đồng dạng với ICM (g-g) (2)
Từ (1) và (2) suy ra (khụng đổi)
c) Chứng minh BHD đồng dạng với DHC (g-g) 	
- Chứng minh DPB đồng dạng với CQD (c-g-c) 
mà 
Bài 10: Cho tam giỏc ABC nhọn cú cỏc đường cao AD,BE,CF cắt nhau tại H.
Tớnh tổng: 
Chứng minh: BH.BE + CH.CF = BC
Chứng minh: H cỏch đều ba cạnh tam giỏc DEF.
Trờn cỏc đoạn HB,HC lấy cỏc điểm M,N tựy ý sao cho HM = CN. 
 Chứng minh đường trung trực của đoạn MN luụn đi qua một điểm cố định.
5
a
Trước hết chứng minh: = 
Tương tự cú: ; 
Nờn = = 1
b
Trước hờt chứng minh BDHBEC BH.BE = BD.BC
 Và CDHCFB CH.CF = CD.CB.
 BH.BE + CH.CF = BC.(BD + CD) = BC (đpcm)
c
Trước hết chứng minh: AEF ABC 
 Và CDECAB 
 mà EBAC nờn EB là phõn giỏc của gúc DEF.
 Tương tự: DA, FC là phõn giỏc của cỏc gúc EDF và DFE.
 Vậy H là giao điểm cỏc đường phõn giỏc của tam giỏc DEF 
 nờn H cỏch đều ba cạnh của tam giỏc DEF (đpcm)
d
 Gọi O là giao điểm của cỏc đường trung trực của hai đoạn MN và HC, ta cú OMH = ONC (c.c.c) .(1)
 Mặt khỏc ta cũng cú OCH cõn tại O nờn:.(2)
 Từ (1) và (2) ta cú: HO là phõn giỏc của gúc BHC
 Vậy O là giao điểm của trung trực đoạn HC và p/giỏc của gúc BHC nờn O là điểm cố định. 
 Hay trung trực của đoạn MN luụn đi qua một điểm cố định là O.
Bài 11: Cho hỡnh vuụng ABCD ( AB = a ), M là một điểm bất kỳ trờn cạnh BC. Tia Ax vuụng gúc với AM cắt đường thẳng CD tại K. Gọi I là trung điểm của đoạn thẳng MK. Tia AI cắt đường thẳng CD tại E. Đường thẳng qua M song song với AB cắt AI tại N.
	1/ Tứ giỏc MNKE là hỡnh gỡ ? Chứng minh.
	2/ Chứng minh: AK2 = KC . KE.
	3/ Chứng minh rằng khi điểm M di chuyển trờn cạnh BC thỡ tam giỏc CME luụn cú chu vi khụng đổi.
	4/ Tia AM cắt đường thẳng CD ở G. Chứng minh rằng khụng phụ thuộc vào vị trớ của điểm M.
Cõu 1: 0, 75 điểm.
	+ Từ MN // AB // CD và MI = IK ỏp dụng định lý Ta let ta cú NI = IE
 ( 0,25 điểm )
	+ Chỉ ra tam giỏc AMK vuụng cõn tại A để cú AE KM ( 0,25 điểm )
	+ Tứ giỏc MNKE là hỡnh bỡnh hành cú hai đường chộo vuụng gúc với nhau nờn MNKE là hỡnh thoi. ( 0,25 điểm )
Cõu 2: 0, 75 điểm.
	+ Từ tớnh chất hỡnh vuụng cú ACK = 45 0. ( 0,25 điểm )
	+ Chứng minh hai tam giỏc AKE và CKA đồng dạng, suy ra ĐPCM. ( 0,5 điểm )
Cõu 3: 1, 0 điểm.
	+ Từ hai tam giỏc ABM và ADK bằng nhau ta cú MB = DK nờn EK = MB + ED. ( 0,25 điểm )
	+ Tam giỏc AMK vuụng cõn tại A cú MI = IK nờn AI là trung trực của MK do đú ME = EK. ( 0,25 điểm )
	+ Từ đú ME = MB + ED, suy ra ME + CM + CE = 2a. ( 0,25 điểm )
 + KL: ( 0,25 điểm ) 
Cõu 4: 1, 0 điểm.
	+ Tam giỏc AMK vuụng cõn tại A nờn AM = AK; do đú 
	= . ( 0,25 điểm )
	+ Tam giỏc AKG vuụng tại A nờn AK . AG = KG . AD = 2. dt AKG, do đú AK2 . AG2 = KG2 . AD2. ( 0,25 điểm )
	+ Mặt khỏc lại cú KG2 = AK2 + AG2 và AD = a nờn ta cú 
AK2 . AG2 = a2( AK2 + AG2 ), hay , suy ra = 
 ( 0,25 điểm )
Bài 13 : 
 Cho hỡnh bỡnh hành ABCD , trờn cạnh AB và CD lần lượt lấy cỏc điểm M , K sao cho 
 AM = CK . Lấy điểm P nằm trờn cạnh AD ( P ≠ A ; P ≠ D ). Nối PB , PC cắt MK tại 
 E , F . Chứng minh 
Bài 14:
Cho hình vuông ABCD, độ dài các cạnh bằng a. Một điểm M chuyển động trên cạnh DC (MD, MC) chọn điểm N trên cạnh BC sao cho MAN = 45o, DB thứ tự cắt AM, AN tại E và F.
1. Chứng minh: ° ABF # °AMC
2.Chứng minh AFM = AEN = 90o
3. Chứng minh SAEF = SAMN
4. Chứng minh chu vi tam giác CMN không đổi khi M chuyển động trên DC
5. Gọi H là giao điểm của MF và NE . Chứng Minh: MH.MF + NH.NE = CN2 + CM2
 Giải
Bài 14:
 1. Chứng minh: ° ABF # °AMC ( 1,25 điểm)
-Ta cm: ABF =ACM = 450
-BAF =MAC ( vì cùng cộng với góc CAN bằng 450 )
 suy ra : ° ABF # °AMC
 2. Chứng minh AFM = AEN = 90o ( 1,5 điểm)
TừD AFB # D AMC (g.g) 
=> 
Có MAF =BAC = 45 0(2) 
Từ 1 và 2 => D AFM # D ABC 
=> AFM = ABC = 90o
C/M hoàn toàn tơng tự có AEN = 900 
vì vậy AFM = AEN = 90o
 3. S D AEF = 1/2 S D AMN (2 điểm)
Có D AFM # D AEN => 
=> D AEF # D AMN (c.g.c) => 
Có FAM = 450, AFM = 900 
=> D AFM Vuông cân đỉnh F nên AM2 = AF2 + FM2 = 2AF2 
 => = 
Thay vào (1) ta đợc = hay: S D AEF = 1/2 S D AMN
 4.. C/M chu vi D CMN không đổi ( 1,25 điểm)
 Trên tia đối của tia DC lấy điểm K sao cho DK = BN 
 D ADK = D ABN => AK = AN và BAN = DAK. 
 do đó D AMN = D AKM (c.gc) => MN=KM 
Vì vậy: Chu vi D CMN = MN + CN +CM = CM + KM + CN 
 = CD + KD + CN = CD + NB + CN 
 = CD + CB = 2a không đổi 
Tức là: Chu vi D CMN không thay đổi khi M chuyển động trên cạnh DC
5. Chứng Minh: MH.MF + NH.NE = CN2 + CM2	(2 điểm)
 Kẻ HI ^ MN tại I 
- Cm: ° MHI # ° MNF => MH.MF =MI.MN
- Cm: °NHI # °NME => NH.NE =NI.NM
- suy ra: MH.MF + NH.NE =MI.MN + NI.NM = MN( MI+NI ) = MN2
- áp dụng định lí Pitago vào °CMN ta có: MN2 = MC2 +CN2
 Vậy: MH.MF + NH.NE = MC2 +CN2
Bài 15:Cho tam giỏc ABC nhọn (AB<AC). Cỏc đường cao AE, BF cắt nhau tại H. Gọi M trung điểm của BC, qua H vẽ đường thẳng a vuụng gúc với HM, a cắt AB, AC lần lượt tại I và K.
a. Chứng minh ABC đồng dạng EFC.
b. Qua C kẻ đường thẳng b song song với đường thẳng IK, b cắt AH, AB theo thứ tự tại N và D. Chứng minh NC = ND và HI = HK.
c. Gọi G là giao điểm của CH và AB. Chứng minh:
 Giải
Ta cú AEC BFC (g-g) nờn suy ra 
Xột ABC và EFC cú và gúc C chung nờn suy ra ABC EFC ( c-g-c)
Vỡ CN //IK nờn HM CN M là trực tõm HNC 
MN CH mà CH AD (H là trực tõm tam giỏc ABC) nờn MN // AD
Do M là trung điểm BC nờn NC = ND
IH = IK ( theo Ta let)
Ta cú:
Tương tự ta cú và 
= +. Dấu ‘=’ khi tam giỏc ABC đều, mà theo gt thỡ AB < AC nờn khụng xảy ra dấu bằng.
 Cõu 16 : 
Gọi O là giao điểm hai đường chộo AC và BD của hỡnh thang ABCD (AB//CD). Đường thẳng qua O song song với AB cắt AD và BC lần lượt tại M và N.
 	 a) Chứng minh OM=ON.
 	 b) Chứng minh .
 	 c) Biết Tớnh  ?
 	 d) Nếu . Chứng minh BD > AC.
 hỡnh vẽ
a/ Ta cú Do MN//DCOM=ON.
b/ Do MN//AB và CD và . Do đú: (1)
Tương tự: (2)
Từ (1);(2) 
c/ Hai tam giỏc cú cựng đường cao thỡ tỉ số diện tớch 2 tam giỏc bằng tỉ số giữa 2 cạnh đỏy tương ứng. Do vậy : và 
Nhưng nờn .Tương tự .Vậy 
d/ Hạ AH, BK vuụng gúc với CD tại H và K
Do nờn H, K nằm trong đoạn CD
Ta cú . 
Tứ giỏc BCEA là hỡnh bỡnh hành nờn BC=AE Vậy AD>BC DH>KCDK > CH. 
Theo định lý pitago cho tam giỏc vuụng BKD ta cú : (Do