Bài tập ôn tập môn Toán Lớp 7

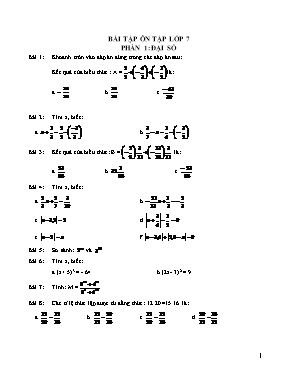
BÀI TẬP ÔN TẬP LỚP 7
PHẦN 1: ĐẠI SỐ
Khoanh tròn vào đáp án đúng trong các đáp án sau:
Kết quả của biểu thức : A =là:
a.	b.	c.
Tìm x, biết:
a.	b.
Kết quả của biểu thức: B = là:
a.	b.	c. 
Tìm x, biết:
a.	b.
c.	d.
e.	f.
So sánh: và 
Tìm x, biết:
a.(x+ 5)3 = - 64	b.(2x- 3)2 = 9
Tính: M =
Các tỉ lệ thức lập được từ đẳng thức: 12.20 =15.16 là:
a.	b.	c.	d.
Tìm tỉ số , biết x, y thoả mãn:
Tìm x , y biết : và x + y = 70
Tìm sai lầm trong lời giải sau và sửa lại chỗ sai:
a); ; 
b)(; ; 
c)= 0,1; ; 
Tìm x Q, biết:
a. x2 + 1 = 82	b. x2 	c. (2x+3)2 = 25
Mẹ bạn Minh gửi tiền tiết kiệm 2 triệu đồng theo thể thức “có kì hạn 6 tháng”. Hết thời hạn 6 tháng, mẹ Minh được lĩnh cả vốn lẫn lãi là 2 062 400. Tính lãi suất hàng tháng của thể thức gửi tiết kiệm này.
Theo hợp đồng, hai tổ sản xuất chia lãi với nhau theo tỉ lệ 3:5. Hỏi mỗi tổ được chia bao nhiêu nếu tổng số lãi là: 12 800 000 đồng.
Trong mặt phẳng toạ độ vẽ tam giác ABC với các đỉnh A(3; 5); B(3; -1); C(-5; -1). Tam giác ABC là tam giác gì?
Vẽ trên cùng một hệ trục toạ độ Oxy các đồ thị của các hàm số:
a) y = - 2x;	b) y = 	c) y =x
Viết biểu thức đại số biểu diễn:
a. Hiệu của a và lập phương của b.
b. Hiệu các lập phương của a và b.
c. Lập phương của hiệu a và b.
Tính giá trị của biểu thức:
A = 3x2 + 2x – 1 tại = 
B = 3x2y + 6x2y2 + 3xy2 tại x =, y =
Cho 3 đơn thức sau:
; 	;	
a. Tính tích của 3 đơn thức trên.
b. Tính giá trị của mỗi đơn thức và giá trị của đơn thức tích tại x= -1, y = -2; z = 3.
Thu gọn các đa thức sau rồi tìm bậc của đa thức.
a. 3y(x2- xy) – 7x2(y + xy)
b. 4x3yz - 4xy2z2 – (xyz +x2y2z2) ( a+1), với a là hằng số.
Cho các đa thức :
A = 4x2 – 5xy + 3y2;
B = 3x2 +2xy + y2;
C = - x2 + 3xy + 2y2
Tính: A + B + C; 	B – C – A; 	C- A – B.
Tìm đa tức M, biết:
a. M + ( 5x2 – 2xy ) = 6x2+ 9xy – y2
b. M – (3xy – 4y2) = x2 -7xy + 8y2
c. (25x2y – 13 xy2 + y3) – M = 11x2y – 2y2;
d. M + ( 12x4 – 15x2y + 2xy2 +7 ) = 0
Cho các đa thức :
A(x) = 3x6 – 5x4 +2x2- 7
B(x) = 8x6 + 7x4 – x2 + 11
C(x) = x6 + x4 – 8x2 + 6
Tính: A(x) + B(x); 	B(x) + C(x); 	A(x) + C(x)
	A(x) + B(x)- C(x); 	B(x) + C(x) – A(x);
	C(x) + A(x) - B(x); 	A(x) + B(x) + C(x)
Tìm một nghiệm của mỗi đa thức sau:
f(x) = x3 – x2 +x -1
g(x) = 11x3 + 5x2 + 4x + 10
h(x) = -17x3 + 8x2 – 3x + 12.
Tìm nghiệm của đa thức sau:
x2 + 5x
3x2 – 4x
5x5 + 10x
x3 + 27
Cho đa thức: f(x) = x4 + 2x3 – 2x2 - 6x – 5
	Trong các số sau: 1, -1, 5, -5 số nào là nghiệm của đa thức f(x)
Cho hai đa thức:	 P(x) = x2 + 2mx + m2
	Q(x) = x2 + (2m + 1)x + m2
Tìm m, biết P(1) = Q(-1)
Cho đa thức: Q(x) = ax2 + bx + c
Biết 5a + b + 2c = 0. Chứng tỏ rằng Q(2).Q(-1) 0
Biết Q(x) = 0 với mọi x. Chứng tỏ rằng a = b = c = 0.
Thời gian làm bài tập của các hs lớp 7 tính bằng phút đươc thống kê bởi bảng sau:
4
5
6
7
6
7
6
4
6
7
6
8
5
6
9
10
5
7
8
8
9
7
8
8
8
10
9
11
8
9
8
9
4
6
7
7
7
8
5
8
Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
Lập bảng tần số? Tìm mốt của dấu hiệu?Tính số trung bình cộng?
Vẽ biểu đồ đoạn thẳng?
Một GV theo dõi thời gian làm bài tập (thời gian tính theo phút) của 30 HS của một trường (ai cũng làm được) người ta lập bảng sau:
Thời gian (x)
5
7
8
9
10
14
Tần số (n)
4
3
8
8
4
3
N = 30
a) Dấu hiệu là gì? Tính mốt của dấu hiệu?
b) Tính thời gian trung bình làm bài tập của 30 học sinh?
c) Nhận xét thời gian làm bài tập của học sinh so với thời gian trung bình.
Một cửa hàng bán Vật liệu xây dựng thống kê số bao xi măng bán được hàng ngày ( trong 30 ngày ) được ghi lại ở bảng sau.
20
35
15
20
25
40
25
20
30
35
30
20
35
28
30
15
30
25
25
28
20
28
30
35
20
35
40
25
40
30
Dấu hiệu mà cửa hàng quan tâm là gì ? Số các giá trị là bao nhiêu ?
Lập bảng “tần số”.
Hãy vẽ biểu đồ đoạn thẳng, rồi từ đó rút ra một số nhận xét.
Hỏi trung bình mỗi ngày cửa hàng bán được bao nhiêu bao xi măng ? Tìm mốt của dấu hiệu.
Điểm kiểm tra Toán ( 1 tiết ) của học sinh lớp 7B được lớp trưởng ghi lại ở bảng sau:
Điểm số (x)
3
4
5
6
7
8
9
10
Tần số (n)
1
2
6
13
8
10
2
3
N = 45
Dấu hiệu ở đây là gì ? Có bao nhiêu học sinh làm bài kiểm tra ?
Hãy vẽ biểu đồ đoạn thẳng và rút ra một số nhận xét.
Tính điểm trung bình đạt được của học sinh lớp 7B. Tìm mốt của dấu hiệu.
Điểm trung bình môn Toán cả năm của các học sinh lớp 7A được cô giáo chủ nhiệm ghi lại như sau:
6,5
7,3
5,5
4,9
8,1
5,8
7,3
6,5
5,5
6,5
7,3
9,5
8,6
6,7
9,0
8,1
5,8
5,5
6,5
7,3
5,8
8,6
6,7
6,7
7,3
6,5
8,6
8,1
8,1
6,5
6,7
7,3
5,8
7,3
6,5
9,0
8,0
7,9
7,3
5,5
Dấu hiệu mà cô giáo chủ nhiệm quan tâm là gì ? Có bao nhiêu bạn trong lớp 7A ?
Lập bảng “tần số”. Có bao nhiêu bạn đạt loại khá và bao nhiêu bạn đạt loại giỏi ?
Tính điểm trung bình môn Toán cả năm của học sinh lớp 7A . Tìm mốt của dấu hiệu.
Thu gọn đơn thức, tìm bậc, hệ số.
	K = 	 L =
Thu gọn các đơn thức sau, rồi tìm hệ số, phần biến, bậc của chúng:
	a) 2x2yz.(-3xy3z) ; 	b) (-12xyz).( x2yz3)y; 
	c)5ax2yz(-8xy3 bz)2 ( a, b là hằng số cho trước); 	d) 15xy2z(x2yz3)3.2xy
Cho các đơn thức : 2x2y3 ; 5y2x3 ; - x3 y2 ; - x2y3 
a) Hãy xác định các đơn thức đồng dạng . b)Tính đa thức F là tổng các đơn thức trên 
c) Tìm giá trị của đa thức F tại x = -3 ; y = 2.
d) Nhân các đơn thức đã cho rồi tìm bậc, phần biến, hệ số của đơn thức tích.
Hãy sắp xấp các đơn thức sau theo từng nhóm các đơn thức đồng dạng với nhau, rồi cộng các đơn thức đồng dạng đó:
Thu gọn đa thức, tìm bậc.
Tính tổng và hiệu của hai đa thức và tìm bậc của đa thức thu được .
a)	A = 4x2 – 5xy + 3y2 ; 	B = 3x2 + 2xy - y2
Tìm đa thức M, biết :
 a) M + (5x2 – 2xy) = 6x2 + 9xy – y2 	 b) M + (3x2 y − 2xy3 ) = 2x2 y − 4xy3	
Cho đa thức A = −2 xy 2 + 3xy + 5xy 2 + 5xy + 1 – 7x2 – 3y2 – 2x2 + y2
	 B = 5x2 + xy – x2 – 2y2
a) Thu gọn đa thức A, B. Tìm bậc của A, B.
b) Tính giá trị của A tại x = ; y =-1
c) Tính C = A + B. Tính giá trị của đa thức C tại x = -1; y = - ½.
d) Tìm D = A – B. 
Thu gọn đa thức, tìm bậc.
Tính tổng và hiệu của hai đa thức và tìm bậc của đa thức thu được .
.
Tìm đa thức M, biết :
a) b) 
Tính tổng và hiệu của hai đa thức sau:
a) A(x) = 3x4 – x3 + 2x2 – 3	; B(x) = 8x4 + x3 – 9x + 	
Tính : A(x) + B(x); 	A(x) - B(x); 	B(x) - A(x);
 b) 
	Tính C(x) + D(x) ; C(x) - D(x) ; D(x) - C(x) 
Cho 2 đa thức : P(x) = - 2x2 + 3x4 + x3 +x2 - x
 Q(x) = 3x4 + 3x2 - - 4x3 – 2x2
Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm dần của biến. Tìm bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức.
Tính P(x) + Q(x); P(x) - Q(x); Q(x) – P(x).
 Đặt M(x) = P(x) - Q(x). Tính M(-2).
Chứng tỏ x = 0 là nghiệm của đa thức P(x), nhưng không phải là nghiệm của đa thức Q(x)
Cho 3 đa thức : 
 M(x) = 3x3 + x2 + 4x4 – x – 3x3 + 5x4 + x2 – 6 
 N(x) = - x2 – x4 + 4x3 – x2 -5x3 + 3x + 1 + x 
	P(x) = 1 + 2x5 – 3x2 + x5 + 3x3 – x4 – 2x
a) Tính : M(x) + N(x) + P(x) ; 
b) Tính M(x) – N(x) – P(x) 
Cho đa thức P(x) = ax3 – 2x2 + x – 2(a là hằng số cho trước)
a) Tìm bậc, hệ số cao nhất, hệ số tự do của P(x).
b) Tính giá trị của P(x) tại x = 0.
c) Tìm hằng số a thích hợp để P(x) có giá trị là 5 tại x = 1.
Tính tổng và hiệu của hai đa thức sau:
 a) 
	Tính P(x) + Q(x) ; P(x) - Q(x) ; Q(x) - P(x) 
 b) 
	 Tính M(x) + N(x) ; M(x) - N(x) ; N(x) - M(x) 
Cho 2 đa thức : P(x) = - x2 + 5x4 + 2x3 +x2 - x
 Q(x) = 7x4 + 2x2 - - 4x3 – 6x2
a.Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm dần của biến. Tìm bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức.
b.Tính P(x) + Q(x); P(x) - Q(x); Q(x) – P(x).
c. Đặt M(x) = P(x) - Q(x). Tính M(-2).
Cho 2 đa thức : 
 M(x) = 3x3 + x2 + 4x4 – x – 3x3 + 5x4 + x2 – 6 
	P(x) = 1 + 2x5 – 3x2 + x5 + 3x3 – x4 – 2x
a) Tính : M(x) + P(x) ; 
b) Tính M(x) – ) P(x 
Tính giá trị của biểu thức sau tại x = 1; y = -1; z = 3
a) (x2y – 2x – 2z)xy	b) 
Thu gọn các đơn thức:
a) 	b) -54y2 . bx ( b là hằng số)	c) 
Cho hai đa thức : 
Hãy thu gọn và sắp xếp hai đa thức trên.
Tính f(x) + g(x) và f(x) - g(x)
Cho đa thức f(x) = -15x3 + 5x4 – 4x2 +8x2 – 9x3 – x4 + 15 – 7x3 
Thu gọn đa thức trên.
Tính f(1) ; f(-1)
Tìm nghiệm của đa thức sau: 
a/ x2 -4 b/ x2+ 9 c/ ( x- 3) ( 2x + 7 ) d/ |x| +x e/ |x| - x
Tìm giá trị nhỏ nhất của các biểu thức sau: 
 a/ (x – 3,5)2+ 1 b/( 2x – 3)4 – 2
Tìm giá trị lớn nhất của biểu thức sau:
 a/ - x2 : b/ -( x - )2 + 1
Cho P(x) = 100x100 +99x99 + 98x98 +  + 2x2 + x . Tính P(1)
Cho P(x) = x99 – 100x98 +100x97 – 100x96 + +100x – 1 .Tính P(99)
PHẦN 2: HÌNH HỌC
Chọn câu phát biểu đúng trong các câu sau:
a) Hai góc đối đỉnh thì bằng nhau.
b) Hai góc bằng nhau mà chung đỉnh thì đối đỉnh.
c) Nếu hai góc kề bù nhau thì hai tia phân giác của chúng vuông góc với nhau.
d) Nếu hai đường thẳng cắt một đường thẳng thứ ba thì hai góc so le trong bằng nhau.
Cho biếtc.Trong góc AOB vẽ các tia OM và ON sao cho:
OA OM, OBON.
a) Tính số đo các góc: AOM, BON.
b) Chứng minh: 
Chọn câu phát biểu đúng trong các câu sau:
a) Trong một tam giác, không thể có hai góc tù.
b) Góc ngoài của tam giác phải là góc tù.
c) Nếu cạnh đáy và góc đối diện với cạnh ấy của tam giác cân này bằng cạnh đáy và góc đối diện với cạnh ấy của tam giác cân kia thì hai tam giác đó bằng nhau.
d) Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau.
Cho tam giác ABC cân tại A. Điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chứng minh rằng:
a. BE = CD 
b. Tam giác KBD bằng tam giác KCE
c. AK là phân giác của góc A
d. Tam giác KBC cân
Cho tam giác ABC ; = 600, AB = 7cm, BC = 15cm.Trên cạnh BC lấy điểm D sao cho = 600. Gọi H là trung điểm của BD.
a. Tính độ dài HD
b. Tính độ dài AC.
c. Tam giác ABC có phải là tam giác vuông hay không?
Cho tam giác ABC vuông ở A, có AB = 5cm, BC = 13. Ba đường trung tuyến AM, BN, CE cắt nhau tại O.
Tính AM, BN, CE.
Tính diện tích tam giác BOC
Cho tam giác ABC, ba đường trung tuyến AD, BE, CF. Từ E kẻ đường thẳng song song với AD cắt ED tại I.
Chứng minh IC // BE.
Chứng minh rằng nếu AD vuông góc với BE thì tam giác ìC là tam giác vuông.
Cho tam giác ABC ; góc A = 900 ; AB = 8cm; AC = 15 cm
Tính BC
Gọi I là giao điểm các tia phân giác của tam giác ABC.Tính khoảng cách từ điểm I đến các cạnh của tam giác.
Cho tam giác ABC cân tại A, góc A bằng 400. Đường trung trực của AB cắt BC ở D.
Tính góc CAD.
Trên tia đối của tia AD lấy điểm M sao cho AM = CD. Chứng minh tam giác BMD cân.
Cho tam giác ABC vuông ở A, đường cao AH, phân giác AD. Gọi I, J lần lượt là các giao điểm các đường phân giác của tam giác ABH, ACH; E là giao điểm của đường thẳng BI và AJ. Chứng minh rằng:
Tam giác ABE vuông
IJ vuông góc với AD
Cho tam giác đều AOB, trên tia đối của tia OA, OB lấy theo thứ tự các điểm C và D sao cho OC = OD. Từ B kẻ BM vuông góc với AC, CN vuông góc với BD. Gọi P là trung điểm của BC.Chứng minh:
a. Tam giác COD là tam giác đều
b. AD = BC
c. Tam giác MNP là tam giác đều
Cho tam giác cân ABC, AB = AC, đường cao AH. Kẻ HE vuông góc với AC. Gọi O là trung điểm của EH, I là trung điểm của EC. Chứng minh:
IO vuông góc vơi AH
AO vuông góc với BE
Cho tam giác nhọn ABC. Về phía ngoài của tam giác vẽ các tam giác vuông cân ABE và ACF ở B và C.Trên tia đối của tia AH lấy điểm I sao cho 
AI = BC. Chứng minh:
Tam giác ABI bằng tam giác BEC
BI = CE và BI vuông góc với CE.
Ba đường thẳng AH, CE, BF cắt nhau tại một điểm. 
Cho tam giác ABC vuông tại A, có 
AB < AC. Trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH vuông góc với BC, kẻ DK vuông góc với AC.
 a)Chứng minh : ; 
b)Chứng minh : AD là phân giác của góc HAC 
c) Chứng minh : AK = AH. 
Cho tam giác DEF vuông tại D, phân giác EB . Kẻ BI vuông góc với EF tại I . Gọi H là giao điểm của ED và IB .Chứng minh:
a) EDB = EIB 
b) HB = BF 
c) DB<BF
d) Gọi K là trung điểm của HF. Chứng minh 3 điểm E, B, K thẳng hàng
Cho tam giác ABC vuông tại A, AH là đường cao. Trên tia đối của tia AH lấy điểm D sao cho AD = AH . Gọi E là trung điểm của HC, F là giao điểm của DE và AC.
	a/ Chứng minh rằng HF cát CD tại trung điểm của CD.
	b/ Chứng minh HF = 1/3 CD.
c/ Gọi I là trung điểm AH. Chứng minh EI vuông góc với AB
Cho hình vẽ sau
 biết . 
Chứng minh rằng Ax // Cy
Với hình vẽ sau. 
Biết . 
Chứng minh rằng Ax // Cy
Tính số đo x của góc O ở hình sau : 
Cho tam giác ABC có , trên cạnh BC lấy điểm E
sao cho BE = BA. Tia phân giác của góc B cắt AC ở D. 
So sánh các độ dài DA và DE.
Tính số đo góc BED.
Gọi I là giao điểm của AE và BD. 
 Chứng minh rằng BD là đường trung trực của AE
Cho tam giác ABC có . Tia phân giác của góc B cắt AC ở D.
Trên tia đối của tia BD lấy điểm E sao cho BE = AC.
Trên tia đối của tia CB lấy diểm K sao cho CK = AB.
Chứng minh : 
Chứng minh rằng EK = AK.
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD 
vuông góc với AB và bằng AB ( D khác phía C đối với AB),
vẽ đoạn thẳng AE vuông góc với AC và bằng AC 
( E khác phía B đối với AC). Chứng minh rằng 
 a) DC = BE
 b) DC BE.
Cho tam giác ABC. Gọi K, D lần lượt là trung điểm của các cạnh AB, BC. Trên tia đối của tia DA lấy điểm M sao cho DM = DA. Trên tia đối của tia KM lấy điểm N sao cho KN = KM. Chứng minh 
 a) 
 b) 
 c) A là trung điểm của đoạn thẳng NC
Cho tam giác ABC vuông tại A có AB = AC. Qua A đường thẳng xy ( B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng:
 a) 
 b) DE = BD + CE. 
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC, vẽ điểm F sao cho E là trung điểm của DF.
Chứng minh rằng:
 DB = CF
 DE // BC và 
Cho góc xOy khác góc bẹt. Trên tia Ox lần lượt lấy hai điểm B và C, trên tia Oy lần lượt lấy hai điểmA và D sao cho OA = AB, OD = OC. Gọi I là giao điểm của AC và BD.
Chứng minh 
AI = IB
OI là tia phân giác của góc xOy
Cho tam giác ABC. vẽ phía ngoài các tam giác ABC các tam giác vuông tại A là ABD, ACE có AB = AD, AC = AE.
 Kẽ AH BC, DM AH, EN AH. Chứng minh rằng:
DM = AH
EN = AH. Có nhận xét gì về DM và EN
Gọi O là giao điểm của AN và DE.
 Chứng minh rằng O là trung điểm của DE 
Cho tam giác nhọn ABC, kẻ AH vuông góc BC. Tính chu vi của tam giác ABC biết
AC = 20cm, AH = 12cm, BH = 5cm
Tính độ dài các cạnh góc vuông của tam giác vuông cân có cạnh huyền bằng:
 2cm
Cho hình vẽ sau trong đó.
 Tính AB biết AE = 4m, AC = 5m, BC = 9m.
Cho tam giác ABC vuông tại A . Trên tia đối của tia AC lấy điểm D sao cho AC =AD . Trêntia đối của tia BA lấy điểm M bất kỳ . Chứng minh rằng :
a/ BA là tia phân giác của góc CBD. b/ DMBD = DMBC
Cho tam giác ABC có , Đường cao AH 
a/ Chứng minh AH < ( AB + AC )
b/ Hai đường trung tuyến BM , CN cắt nhau tại G Trên tia đối của tia MB lấy điểm E sao cho ME =MG . Trên tia đối của tia NC lấy điểm F sao cho NF = NG . Chứng minh : EF= BC 
c/Đường thẳng AG cắt BC tại K Chứng minh 
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho 
AD = AE.
Chứng minh rằng BE = CD.
Gọi O là giao điểm của BE và CD. Chứng minh rằng 
Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng :
AD = EF.
AE = EC.
Cho góc x0y , M là điểm nằm trên tia phân giác 0z của góc x0y. Trên các tia 0x và 0y lần lượt lấy hai điểm A và B sao cho OA = OB. Chứng minh rằng: 
a/ MA =MB 
 	b/ Đường thẳng chứa tia phân giác Oz là đường trung trực của đoạn thẳng AB
c/ Gọi I là giao điểm của AB và 0z . Tính OI biết AB = 6cm OA = 5cm.
Cho góc nhọn x0y. Trên hai cạnh 0x và 0y lần lượt lấy hai điểm A và B sao cho OA = OB . Tia phân giác của góc x0y cắt AB tại I.
a/ Chứng minh OI ^ AB.
b/ Gọi D là hình chiếu của điểm A trên 0y. C là giao điểm của AD với OI .Chứng minh:BC ^0x
c/Giả sử = 600 , OA = OB = 6cm . Tính độ dài đoạn thẳng OC
Cho tam giác ABC cân tại A, đường cao AH . Biết AB = 5cm BC =6cm 
a/ Tính độ dài các đoạn thẳng BH , AH.
b/ Gọi G là trọng tâm của tam giác ABC . Chứng minh rằng ba điểm A, G, H thẳng hàng 
c/ Chứng minh : 
Cho tam giác ABC cân tại A . Gọi G là trọng tâm , I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh :
a/ Ba điểm A ,G ,I thẳng hàng 
b/ BG < BI < BA
c/ 
d/ Xác định vị trí của điểm M sao cho tổng các độ dài BM + MC có giá trị nhỏ nhất
Cho điểm M nằm trong tam giác ABC . Chứng minh rằng tổng MA +MB +MC lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tam giác ABC.