2 Đề kiểm tra học kỳ I Toán 8 - Năm học 2022-2023 - Trường PTDTBT TH&THCS Tà Củ Tỳ 1 (Có đáp án + Ma trận)

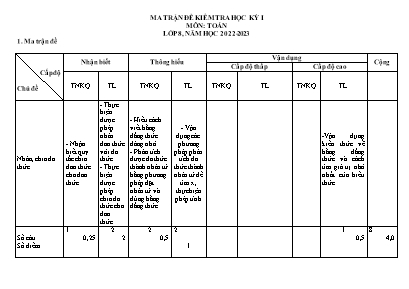
 MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I
 MÔN: TOÁN
 LỚP 8, NĂM HỌC 2022-2023
1. Ma trận đề
 Vận dụng
 Nhận biết Thông hiểu Cộng
 Cấp độ thấp Cấp độ cao
 Cấp độ
Chủ đề TNKQ TL TNKQ TL TNKQ TL TNKQ TL
 - Thực 
 hiện 
 được - Hiểu cách 
 phép viết hằng - Vận 
 nhân đẳng thức dụng các -Vận dụng 
 - Nhận đơn thức đáng nhớ. phương kiến thức về 
 biết quy với đa - Phân tích pháp phân hằng đẳng 
Nhân, chia đa tắc chia thức. được đa thức tích đa thức và cách 
thức đơn thức - Thực thành nhân tử thức thành tìm giá trị nhỏ 
 cho đơn hiện bằng phương nhân tử để nhất của biểu 
 thức. được pháp đặt tìm x, thức.
 phép nhân tử và thực hiện 
 chia đa dùng hằng phép tính.
 thức cho đẳng thức.
 đơn 
 thức.
 1 2 2 2 1 8
Số câu 0,25 2 0,5 0,5 4,0
Số điểm 1 Biết cách - Vận - Vận dụng 
 cộng các dụng kiến quy tắc chia đa 
 phân thức thức tìm thức cho đơn 
 đơn giản. điều kiện thức tìm các 
 để phân giá trị nguyên 
 thức có của biến n để 
Phân thức nghĩa. biểu thức chia 
 - Vận hết cho giá trị 
 dụng quy của biểu thức.
 tắc cộng 
 hai phân 
 thức cùng 
 mẫu.
 1 2 1 4
Số câu
 2 0,5 2,75
Số điểm
 0,25
 Nhận biết Hiểu thế nào -Vận dụng định lí 
 được dấu là tâm đối đường trung bình 
 hiệu nhận xứng của một của tam giác để 
 biết các tứ hình. tính độ dài của 
 giác đặc một cạnh.
Tứ giác biệt. -Vận dụng dấu 
 hiệu nhận biết 
 hình thang và 
 hình thang cân để 
 chứng minh. 
 (PISA)
 1 1 2 4
Số câu
 0,5 0,25 1,5 2,25
Số điểm
 Biết cách tính Vận dụng công 
Đa giác – diện 
 diện tích tam thức tính diện tích 
tích đa giác
 giác vuông. tam giác. 1 1 2
Số câu
 0,25 0,5 0,75
Số điểm
 5 8 5 18
Tổng số câu
 3 4 3 10
Tổng số điểm PHÒNG GD & ĐT BẮC HÀ ĐỀ THI HỌC KÌ I
 TRƯỜNG PTDTBT TIỂU HỌC Môn: Toán 
 VÀ THCS TẢ CỦ TỶ 1 Lớp 8, Năm học: 2022 - 2023
 Thời gian: 90p ( Không kể thời gian 
 giao đề)
 ĐỀ 1
 I. TRẮC NGHIỆM: ( 2đ)
 Hãy khoanh tròn vào chữ cái đứng trước câu trả lời đúng
 Câu 1. Kết quả của phép tính 16x2y5z: 4x2y5 là
 A. 4x B. 4z C. 16x D. 1
 Câu 2. Biểu thức C3 – D3 bằng
 A. (C + D) (C2 – CD + D2) B. (C - D) (C2 + CD + D2)
 C. (C - D) (C2 + CD - D2) D. (C - D) (C2 – CD + D2)
 Câu 3. Phân tích đa thức x2 – 2x + 1 thành nhân tử ta được kết quả là
 A. x( x2 1) B. x(x - 1) 2 C. (x - 1) 2 D. (x + 1) 2 
 Câu 4. Kết quả của phép tính 2x + 2x bằng
 3x2 y2 3x2 y2
 2 2
 A. 2 B. C. 2x D. x
 3y 3xy 3xy
 Câu 5. Trong các hình sau hình nào không có tâm đối xứng
 A. Hình chữ nhât. B. Hình thang cân 
 C. Hình vuông D. Hình bình hành
 Câu 6. Khẳng định nào sau đây là đúng
 A. Hình thang cân có hai đường chéo cắt nhau tại trung điểm của mỗi đường 
là hình chữ nhật.
 B. Hình thang cân có một góc vuông là hình vuông
 C. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
 D. Tứ giác có bốn cạnh bằng nhau là hình chữ nhật.
 Câu 7. Cho tam giác ABC vuông tại A, có AB = 3 cm, BC = 5 cm. Diện tích 
tam giác ABC bằng
 A. 12 cm 2 B. 24 cm 2 C. 10 cm 2 D. 6 cm 2
 II. Tự luận (8đ)
 Câu 8. (2đ) Thực hiện phép tính
 a. x2(x - 2) 
 b. (20x3 - 5x2 + 5x): x 
 Câu 9. (1đ) 
 a. Tìm x biết x2 – 3x = 0
 b. Phân tích đa thức sau thành nhân tử: x2 + xy - x – y
 Câu 10(2đ). Cho biểu thức P = + 
 a. Tìm điều kiện của x để Q xác định.
 b. Rút gọn biểu thức Q. Câu 11(2đ). Mảnh vườn 
 Nhà bạn Hoa có một mảnh vườn hình tam giác ABC vuông tại A với độ dài 
các cạnh AB = 3 m, AC = 6 m. Hoa sử dụng lưới theo hai điểm E; M ( E là trung 
điểm của AC và M là trung điểm của BC) để chia mảnh vườn thành hai phần trồng 
rau và hoa . 
 Câu hỏi mảnh vườn: 
 a. Tính độ dài lưới phải dùng?
 b. Mảnh vườn AEMB là hình gì, vì sao?
 c. Tính diện tích mảnh vườn EMC?
 Câu 12(1đ)
 a. Tìm giá trị nhỏ nhất của đa thức P = y2 - 2y + 2
 b. Tìm giá trị nguyên của x để đa thức A = 8x3 + 4x2 + 3 chia hết cho đa 
thức B = 2x +1. PHÒNG GD & ĐT BẮC HÀ ĐỀ THI HỌC KÌ I
 TRƯỜNG PTDTBT TIỂU HỌC Môn: Toán 
 VÀ THCS TẢ CỦ TỶ 1 Lớp 8, Năm học: 2022 - 2023
 Thời gian: 90p ( Không kể thời gian giao 
 đề)
 ĐỀ 2
 I. TRẮC NGHIỆM: ( 2đ)
 Hãy khoanh tròn vào chữ cái đứng trước câu trả lời đúng
 Câu 1. Kết quả của phép tính 7x5y2: 7y2 là
 A. 7x B. x5 C. 2x5 D. 1
 Câu 2. Biểu thức A3 B3 bằng
 A. (A+B) ( A2 AB B2 ) B. (A - B) ( A2 AB B2 ) 
 C. (A - B) ( A2 AB B2 ) D. (A + B) ( A2 AB B2 ) 
 Câu 3. Phân tích đa thức x2 - 4x + 4 thành nhân tử ta được kết quả là
 A. 4x( x2 1) B. (x +2) 2
 C. 4(x - 1) 2 D. (x - 2) 2 
 Câu 4. Kết quả của phép tính bằng 
 2
 A. B. 4x C. 4x D. 
 3x2 y2 3xy
 Câu 5. Trong các hình sau hình nào không có tâm đối xứng
 A. Hình bình hành B. Hình chữ nhât. 
 C. Hình vuông D. Hình thang cân
 Câu 6. Khẳng định nào sau đây là đúng
 A. Tứ giác có 3 góc vuông là hình chữ nhật.
 B. Hình bình hành có một góc vuông là hình vuông
 C. Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình 
bình hành.
 D. Tứ giác có hai cạnh đối song song là hình bình hành.
Câu 7. Cho tam giác ABC vuông tại A, có AB = 4 cm, BC = 5 cm. Diện tích tam 
giác ABC bằng
 A. 4,5 cm 2 B. 7,5 cm 2 C. 15 cm 2 D. 6 cm 2
 II. Tự luận (8đ)
 Câu 8. (2đ) Thực hiện phép tính
 a. x(x 2 - 3) 
 b. (2x5 + 8x2y - 2x) : 2x
 Câu 9. (1đ) 
 a. Tìm x biết x2 - 4x = 0
 b. Phân tích đa thức sau thành nhân tử: x3 + x2 - 2x - 2
 Câu 10(2đ). Cho biểu thức 
 a. Tìm điều kiện của y để Q xác định.
 b. Rút gọn biểu thức Q. Câu 11(2đ). Mảnh vườn 
 Nhà bạn Mai có một mảnh vườn hình tam giác ABC vuông tại A với độ dài 
các cạnh AB = 2 m, AC = 6 m. Mai sử dụng lưới theo hai điểm E; M ( E là trung 
điểm của AC và M là trung điểm của BC) để chia mảnh vườn thành hai phần trồng 
rau và hoa . 
 Câu hỏi mảnh vườn: 
 a. Tính độ dài lưới phải dùng?
 b. Mảnh vườn AEMB là hình gì, vì sao?
 c. Tính diện tích mảnh vườn EMC?
 Câu 12(1đ). 
 a. Tìm giá trị nhỏ nhất của đa thức P = x2 - 4x + 7 
 b. Tìm giá trị nguyên của n để A = 3n3 + 6n2 + 5 chia hết cho B = n +1. PHÒNG GD & ĐT BẮC HÀ ĐÁP ÁN VÀ BIỂU ĐIỂM
 TRƯỜNG PTDTBT TIỂU HỌC ĐỀ THI HỌC KÌ I
 VÀ THCS TẢ CỦ TỶ 1 Môn: Toán 
 Lớp 8, Năm học: 2022 - 2023
 ĐỀ 1
 I. TRẮC NGHIỆM: ( 2đ). Mỗi ý đúng được 0,25đ
 Câu 1 2 3 4 5 6 7
 Đáp án B B C B B A,C D
 Điểm 0,25 0,25 0,25 0,25 0,25 0,5 0,25
 II. Tự luận (8đ)
Câu Nội dung Điểm
 a. x2(x - 2) = x 3 - 2x 2 1
 8
 b. (20x3 - 5x2 + 5x): x = 20x2 - 5x + 5 1
 a. x 2 - 3x = 0
  x(x - 3) = 0
 Hoặc x = 0 hoặc x - 3 = 0 => x = 3 0,25
 Vậy x = 0 hoặc x = 3 0,25
 9
 b. x2 + xy - x - y
 = (x2 + xy ) - (x + y) 0,25
 = x(x + y) - ( x + y)
 = (x - 1)(x + y) 0,25
 a. Để Q = + xác định thì x + 1 0  x # - 1 1
 b. Q = + 
 0,25
 10 0,25
 0,25
 0,25
 = y + 1 
 GT ABC vuông tại A; 0,5
 AB = 3m, AC = 6m; B
 dùng lưới EM sao cho 
 AE = EC, BM = MC M
 11 KL a. EM = ?
 b. AEMB là hình gì? 
 Vì sao? A C
 c. SEMC =? E
 a. Xét tam giác ABC ta có EA = EC (gt) MB = MC (gt)
 EM là đường trung bình của tam giác ABC 0,25
 AB
 EM = = 3: 2 = 1,5 m 0,25
 2
 b. Xét tứ giác EMBA có EM // AB (Theo ý a) 0, 25
 (gt)
 Vậy tứ giác EMBA là hình thang vuông. 0,25
 c. Ta có
 + EC = AE (gt)
  EC = AC/2 = 6 : 2 = 3 m
 + ME // AB mà AB  AC ME  AC vậy tam giác CEM 0,25
 vuông tại E
 Diện tích tam giác CEM là
 2
 SCEM = (CE. EM)/2 = (1,5 . 3) : 2 = 2,25(m ) 0,25
 a. Ta có P = y2- 2y + 2 = (y - 1)2 + 1
 Vì (y - 1)2 luôn lớn hơn hoặc bằng 0 nên P luôn lớn hơn hoặc 0,25
 bằng 1
 Vậy giá trị nhỏ nhất của P bằng 1 khi y = 1 0,25
12 b. Ta có A : B = (8x3 + 4x2 + 3) : (2x +1) = 4x2 + 2x + 2 : (2x 0,25
 + 1)
 Để A chia hết cho B thì 2  (2x+1) 
 Mà Ư(2) ={-1; 1; -2; 2} 0,25 
 mà x thuộc giá trị nguyên vậy x = 0; -1 PHÒNG GD & ĐT BẮC HÀ ĐÁP ÁN VÀ BIỂU ĐIỂM
 TRƯỜNG PTDTBT TIỂU HỌC ĐỀ THI HỌC KÌ I
 VÀ THCS TẢ CỦ TỶ 1 Môn: Toán 
 Lớp 8, Năm học: 2022 - 2023
 ĐỀ 2
 I. TRẮC NGHIỆM: ( 2đ). Mỗi ý đúng được 0,25đ
 Câu 1 2 3 4 5 6 7
 Đáp án B B D A D A,C D
 Điểm 0,25 0,25 0,25 0,25 0,25 0,5 0,25
 II. Tự luận (8đ)
Câ Nội dung Điể
u m
 a. x(x 2 - 3) = x3 - 3x 1
 8
 b. (2x3 + 8x2 - 2x) : 2x = x2 + 4x - 1 1
 a. x 2 - 4x = 0
 x(x - 4) = 0 0,25
 x = 0 hoặc x - 4 = 0 0,25
 x = 0 hoặc x = 4 
 9
 vậy x = 0; x = 4 
 b. x2 + x - 2x - 2 = x(x - 2) + (x - 2) 0,25
 = (x - 2)(x + 1) 0,25
 a. Để Q xác định thì y + 1 0 => y # -1 1
 b. 1
 10
 GT ABC vuông tại A; AB B 0,5
 = 2m, AC = 6m; dùng lưới 
 EM sao cho AE = EC, BM 
 = MC M
 KL a. EM = ?
 b. AEMB là hình gì? Vì 
 11 sao? A C
 c. SEMC =? E
 a. Xét tam giác ABC ta có EA = EC (gt)
 MB = MC (gt)
 EM là đường trung bình của tam giác ABC 0,25 
 AB
 EM = =2:2 = 1 m 0,25 
 2 b. Xét tứ giác EMBA có 0, 25
 EM // AB ( Theo ý a) 
 (gt) 0,25
 Vậy tứ giác EMBA là hình thang vuông. 
 c. Ta có
 + EC = AE (gt)
 AC 6
 EC 3(m)
 2 2
 + ME // AB mà AB  AC ME  AC vậy tam giác CEM vuông 0,25
 tại E
 Diện tích tam giác CEM là 
 2
 SCEM = (CE. EM)/2 = (1. 3) : 2 = 1,5(m ) 0,25 
 a. Ta có P = x2 - 4x + 7 = (x -2)2 + 3
 Vì (x -2)2 luôn lớn hơn hoặc bằng 0 nên P luôn lớn hơn hoặc bằng 3. 0,25 
 Vậy giá trị nhỏ nhất của P bằng 3 khi x = 2
 0,25
 A 3n3 10n2 5 4 0,25
12 b. Ta có n2 3n 1 
 B 3n 1 3n 1
 A : B = (3n3 + 6n2 + 5):(n+1) = 3n2 + 3n - 3 + 8:(n+ 1)
 Để A chia hết cho B thì 8  (n+1) 
 Mà Ư(8) = {1; -1;2; -2; 4; -4; 8; -8} 
 n thuộc giá trị nguyên vậy n = 0; 1; 3; 7; -2; -3; -5; -9 0,25
 GIÁO VIÊN DUYỆT CỦA TCM DUYỆT CỦA BGH
 Vàng Seo Dềnh Hoàng Thị Thanh